
【题目】已知![]() ,设命题
,设命题![]() :
:![]() ,方程
,方程![]() 存在实数解;命题
存在实数解;命题![]() :不等式
:不等式![]() 对任意
对任意![]() 恒成立.
恒成立.
(1)若![]() 为真命题,则
为真命题,则![]() 的取值范围;
的取值范围;
(2)若![]() 为假命题,
为假命题,![]() 为真命题,求
为真命题,求![]() 取值范围.
取值范围.
科目:高中数学 来源: 题型:
【题目】某人经营一个抽奖游戏,顾客花费3元钱可购买一次游戏机会,每次游戏中,顾客从标有黑1、黑2、黑3、黑4、红1、红3的6张卡片中随机抽取2张,并根据摸出的卡片的情况进行兑奖,经营者将顾客抽到的卡片情况分成以下类别:![]() :同花顺,即卡片颜色相同且号码相邻;
:同花顺,即卡片颜色相同且号码相邻;![]() :同花,即卡片颜色相同,但号码不相邻;
:同花,即卡片颜色相同,但号码不相邻;![]() :顺子,即卡片号码相邻,但颜色不同;
:顺子,即卡片号码相邻,但颜色不同;![]() :对子,即两张卡片号码相同;
:对子,即两张卡片号码相同;![]() :其它,即
:其它,即![]() ,
,![]() ,
,![]() ,
,![]() 以外的所有可能情况,若经营者打算将以上五种类别中最不容易发生的一种类别对应顾客中一等奖,最容易发生的一种类别对应顾客中二等奖,其他类别对应顾客中三等奖.
以外的所有可能情况,若经营者打算将以上五种类别中最不容易发生的一种类别对应顾客中一等奖,最容易发生的一种类别对应顾客中二等奖,其他类别对应顾客中三等奖.
(1)一、二等奖分别对应哪一种类别?(写出字母即可)
(2)若经营者规定:中一、二、三等奖,分别可获得价值9元、3元、1元的奖品,假设某天参与游戏的顾客为300人次,试估计经营者这一天的盈利.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九大提出对农村要坚持精准扶贫,至2020年底全面脱贫.现有扶贫工作组到某山区贫困村实施脱贫工作.经摸底排查,该村现有贫闲农户100家,他们均从事水果种植,2017年底该村平均每户年纯收入为1万元.扶贫工作组一方面请有关专家对果树进行品种改良,提高产量;另一方面,抽出部分农户从事水果包装、销售工作,其人数必须小于种植的人数.从2018年初开始,该村抽出![]() 户(
户(![]() )从事水果包装、销售.经测算,剩下从事水果种植农户的年纯收入每户平均比上一年提高
)从事水果包装、销售.经测算,剩下从事水果种植农户的年纯收入每户平均比上一年提高![]() ,而从事包装销售农户的年纯收入每户平均为
,而从事包装销售农户的年纯收入每户平均为![]() 万元(参考数据:
万元(参考数据:![]() ).
).
(1)至2020年底,为使从事水果种植农户能实现脱贫(每户年均纯收入不低于1万5千元),则应至少抽出多少户从事包装、销售工作?
(2)至2018年底,该村每户年均纯收人能否达到1.355万元?若能,请求出从事包装、销售的户数;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S-ABCD中,底面ABCD是菱形,![]() ,
,![]() 为等边三角形,G是线段SB上的一点,且SD//平面GAC.
为等边三角形,G是线段SB上的一点,且SD//平面GAC.
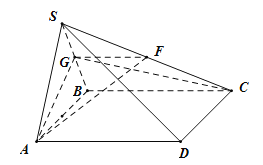
(1)求证:G为SB的中点;
(2)若F为SC的中点,连接GA,GC,FA,FG,平面SAB⊥平面ABCD,![]() ,求三棱锥F-AGC的体积.
,求三棱锥F-AGC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的左焦点为
的左焦点为![]() ,且点
,且点![]() 在C上.
在C上.
![]() 求C的方程;
求C的方程;
![]() 设点P关于x轴的对称点为点
设点P关于x轴的对称点为点![]() 不经过P点且斜率为k的直线l与C交于A,B两点,直线PA,PB分别与x轴交于点M,N,若
不经过P点且斜率为k的直线l与C交于A,B两点,直线PA,PB分别与x轴交于点M,N,若![]() ,求k.
,求k.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线Γ的准线方程为![]() .焦点为
.焦点为![]() .
.
(1)求证:抛物线Γ上任意一点![]() 的坐标
的坐标![]() 都满足方程:
都满足方程:![]()
(2)请求出抛物线Γ的对称性和范围,并运用以上方程证明你的结论;
(3)设垂直于![]() 轴的直线与抛物线交于
轴的直线与抛物线交于![]() 两点,求线段
两点,求线段![]() 的中点
的中点![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
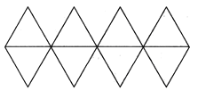
【题目】蹴鞠起源于春秋战国,是现代足球的前身.到了唐代,制作的蹴鞠已接近于现代足球,做法是:用八片鞣制好的尖皮缝制成“圆形”的球壳,在球壳内放一个动物膀胱,“嘘气闭而吹之”,成为充气的球.如图所示,将八个全等的正三角形缝制成一个空间几何体,在几何体内放一个气球,往气球内充气使几何体膨胀,当几何体膨胀成球体(顶点位置不变)且恰好是原几何体外接球时,测得球的体积是![]() ,则正三角形的边长为( )
,则正三角形的边长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com