
ЎѕМвДїЎїґу¶№Ј¬№ЕіЖЭДЈ¬ФІъЦР№ъЈ¬ФЪЦР№ъТСУРОеЗ§ДкФФЕаАъК·ЎЈНо±±¶аЖЅФµШґшЈ¬»ЖєУ№КµАНБµШ·КОЦЈ¬ККТЛЦЦЦІґу¶№ЎЈ2018ДкґєЈ¬ОЄПмУ¦ЦР№ъґу¶№ІОУлКАЅзГіТЧµДѕєХщЈ¬ДіКРЕ©їЖФє»эј«СРѕїЈ¬јУґуУЕБјЖ·ЦЦµДЕаУэ№¤ЧчЎЈЖдЦРТ»По»щґЎ№¤ЧчѕНКЗСРѕїЦзТ№ОВІоґуРЎУлґу¶№·ўСїВКЦ®јдµД№ШПµЎЈОЄґЛїЖСРИЛФ±·Ц±рјЗВјБЛ5МмЦРГїМм100БЈґу¶№µД·ўСїКэµГИзПВКэѕЭ±нёс:
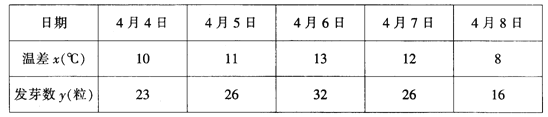
їЖСРИЛФ±И·¶ЁСРѕї·Ѕ°ёКЗ:ґУ5ЧйКэѕЭЦРСЎ3ЧйКэѕЭЗуПЯРФ»Ш№й·ЅіМЈ¬ФЩУГЗуµГµД»Ш№й·ЅіМ¶ФКЈПВµД2ЧйКэѕЭЅшРРјмСй.
(1)ЗуКЈПВµД2ЧйКэѕЭЗЎКЗІ»ПаБЪµД2МмКэѕЭµДёЕВКЈ»
(2)ИфСЎИЎµДКЗ4ФВ5ИХЎў6ИХЎў7ИХИэМмКэѕЭѕЭґЛЗу![]() №ШУЪ
№ШУЪ![]() µДПЯРФ»Ш№й·ЅіМ
µДПЯРФ»Ш№й·ЅіМ![]() Ј»
Ј»
(3)ИфУЙПЯРФ»Ш№й·ЅіМµГµЅµД№АјЖКэѕЭУлКµјККэѕЭµДОуІоѕш¶ФЦµѕщІ»і¬№э1БЈЈ¬ФтИПОЄµГµЅµДПЯРФ»Ш№й·ЅіМКЗїЙїїµДЈ¬ЗлјмСй(ўт)ЦР»Ш№й·ЅіМКЗ·сїЙїїЈї
ЧўЈє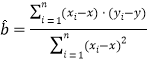
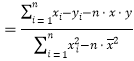 Ј¬
Ј¬![]() .
.
Ўѕґр°ёЎїЈЁ1Ј©![]() Ј»ЈЁ2Ј©
Ј»ЈЁ2Ј©![]() Ј»ЈЁ3Ј©µГµЅµДПЯРФ»Ш№й·ЅіМКЗїЙїїµД
Ј»ЈЁ3Ј©µГµЅµДПЯРФ»Ш№й·ЅіМКЗїЙїїµД
ЎѕЅвОцЎї·ЦОцЈєЈЁ1Ј©АыУГ¶ФБўКВјюµДёЕВК№«КЅЗуЗЎєГКЗІ»ПаБЪµД2МмКэѕЭµДёЕВК.(2)АыУГЧоРЎ¶юіЛ·ЁЗуy№ШУЪ![]() µДПЯРФ»Ш№й·ЅіМОЄ
µДПЯРФ»Ш№й·ЅіМОЄ![]() .ЈЁ3Ј©јмСйјґїЙµГЅв.
.ЈЁ3Ј©јмСйјґїЙµГЅв.
ПкЅвЈє(1)ЗЎєГКЗІ»ПаБЪµД2МмКэѕЭµДёЕВККЗ![]() .
.
(2)УЙКэѕЭµГ![]()
![]() Ј»
Ј»
![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]()
![]() Ј»
Ј»
![]()
![]()
![]() Ј¬
Ј¬
![]()
![]()
![]() Ј»
Ј»
![]()
![]()
![]() Ј¬
Ј¬


![]() Ј»
Ј»
![]()
![]() Ј¬№Кy№ШУЪ
Ј¬№Кy№ШУЪ![]() µДПЯРФ»Ш№й·ЅіМОЄ
µДПЯРФ»Ш№й·ЅіМОЄ![]() .
.
(3)µ±![]() К±Ј¬
К±Ј¬![]()
![]() Ј¬
Ј¬![]() Ј»
Ј»
µ±![]() К±Ј¬
К±Ј¬![]()
![]() Ј¬
Ј¬![]() Ј¬
Ј¬
№КµГµЅµДПЯРФ»Ш№й·ЅіМКЗїЙїїµД.



| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄєЇКэ![]() Ј®
Ј®
ЈЁ1Ј©Иф![]() Ј¬Зу
Ј¬Зу![]() µДµҐµчЗшјдЈ»
µДµҐµчЗшјдЈ»
ЈЁ2Ј©Ц¤ГчЈє![]() Ц»УРТ»ёцБгµгЈ®
Ц»УРТ»ёцБгµгЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎї°С![]() ёцПаН¬µДРЎЗт·ЕµЅИэёц±аєЕОЄ
ёцПаН¬µДРЎЗт·ЕµЅИэёц±аєЕОЄ![]() µДєРЧУЦРЈ¬ЗТГїёцєРЧУДЪµДРЎЗтКэТЄ¶аУЪєРЧУµД±аєЕКэЈ¬Фт№ІУР¶аЙЩЦЦ·Е·ЁЈЁ Ј©
µДєРЧУЦРЈ¬ЗТГїёцєРЧУДЪµДРЎЗтКэТЄ¶аУЪєРЧУµД±аєЕКэЈ¬Фт№ІУР¶аЙЩЦЦ·Е·ЁЈЁ Ј©
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄФІCЈєx2+y2©Ѓ4y+1ЈЅ0Ј¬µгMЈЁ©Ѓ1Ј¬©Ѓ1Ј©Ј¬ґУФІCНвТ»µгPПтёГФІТэТ»МхЗРПЯЈ¬јЗЗРµгОЄTЈ®
ЈЁ1Ј©Иф№эµгMµДЦ±ПЯlУлФІЅ»УЪAЈ¬BБЅµгЗТ|AB|ЈЅ2![]() Ј¬ЗуЦ±ПЯlµД·ЅіМЈ»
Ј¬ЗуЦ±ПЯlµД·ЅіМЈ»
ЈЁ2Ј©ИфВъЧг|PT|ЈЅ|PM|Ј¬ЗуК№|PT|ИЎµГЧоРЎЦµК±µгPµДЧш±кЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ЛДАвЧ¶S©ЃABCDЦРЈ¬MКЗSBµДЦРµгЈ¬ABЎОCDЈ¬BCЎНCDЈ¬ЗТABЈЅBCЈЅ2Ј¬CDЈЅSDЈЅ1Ј¬УЦSDЎНГжSABЈ®
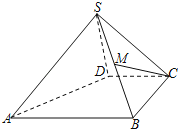
ЈЁ1Ј©Ц¤ГчЈєCDЎНSDЈ»
ЈЁ2Ј©Ц¤ГчЈєCMЎОГжSADЈ»
ЈЁ3Ј©ЗуЛДАвЧ¶S©ЃABCDµДМе»эЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїјЧЎўТТБЅИЛЅшРРПуЖе±ИИьЈ¬Фј¶ЁПИБ¬К¤БЅѕЦХЯЦ±ЅУУ®µГ±ИИьЈ¬ИфИьНк5ѕЦИФОґіцПЦБ¬К¤Ј¬ФтЕР¶Ё»сК¤ѕЦКэ¶аХЯУ®µГ±ИИьЈ®јЩЙиГїѕЦјЧ»сК¤µДёЕВКОЄ![]() Ј¬ТТ»сК¤µДёЕВКОЄ
Ј¬ТТ»сК¤µДёЕВКОЄ![]() Ј¬ёчѕЦ±ИИьЅб№ыП໥¶АБўЈ®
Ј¬ёчѕЦ±ИИьЅб№ыП໥¶АБўЈ®
ЈЁ1Ј©ЗујЧФЪ4ѕЦТФДЪЈЁє¬4ѕЦЈ©У®µГ±ИИьµДёЕВКЈ»
ЈЁ2Ј©УГX±нКѕ±ИИьѕціцК¤ёєК±µДЧЬѕЦКэЈ¬ЗуЛж»ъ±дБїXµД·ЦІјБРєНѕщЦµ.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїСЎРЮ4-4ЈєЧш±кПµУлІОКэ·ЅіМ
ФЪЦ±ЅЗЧш±кПµЦР![]() ЦРЈ¬ЗъПЯ
ЦРЈ¬ЗъПЯ![]() µДІОКэ·ЅіМОЄ
µДІОКэ·ЅіМОЄ![]() ОЄІОКэЈ¬
ОЄІОКэЈ¬ ![]() Ј©. ТФЧш±кФµгОЄј«µгЈ¬
Ј©. ТФЧш±кФµгОЄј«µгЈ¬ ![]() ЦбХэ°лЦбОЄј«ЦбЅЁБўј«Чш±кПµЈ¬ТСЦЄЦ±ПЯ
ЦбХэ°лЦбОЄј«ЦбЅЁБўј«Чш±кПµЈ¬ТСЦЄЦ±ПЯ![]() µДј«Чш±к·ЅіМОЄ
µДј«Чш±к·ЅіМОЄ![]() .
.
ЈЁ1Ј©Йи![]() КЗЗъПЯ
КЗЗъПЯ![]() ЙПµДТ»ёц¶ЇµгЈ¬µ±
ЙПµДТ»ёц¶ЇµгЈ¬µ±![]() К±Ј¬Зуµг
К±Ј¬Зуµг![]() µЅЦ±ПЯ
µЅЦ±ПЯ![]() µДѕаАлµДЧоґуЦµЈ»
µДѕаАлµДЧоґуЦµЈ»
ЈЁ2Ј©ИфЗъПЯ![]() ЙПЛщУРµДµгѕщФЪЦ±ПЯ
ЙПЛщУРµДµгѕщФЪЦ±ПЯ![]() µДУТПВ·ЅЈ¬Зу
µДУТПВ·ЅЈ¬Зу![]() µДИЎЦµ·¶О§.
µДИЎЦµ·¶О§.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎї(2016Ў¤№уСфµЪ¶юґОБЄїј)ФЪЎчABCЦРЈ¬ЅЗAЈ¬BЈ¬CµД¶Ф±Я·Ц±рОЄaЈ¬bЈ¬cЈ¬ПтБїmЈЅ(aЈ«bЈ¬sin AЈsin C)Ј¬ПтБїnЈЅ(cЈ¬sin AЈsin B)Ј¬ЗТmЎОn.
(1)ЗуЅЗBµДґуРЎЈ»
(2)ЙиBCµДЦРµгОЄDЈ¬ЗТADЈЅ![]() Ј¬ЗуaЈ«2cµДЧоґуЦµј°ґЛК±ЎчABCµДГж»эЈ®
Ј¬ЗуaЈ«2cµДЧоґуЦµј°ґЛК±ЎчABCµДГж»эЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄНЦФІ![]() µДБЅёцЅ№µгКЗ
µДБЅёцЅ№µгКЗ![]() Ј¬
Ј¬ ![]() Ј¬ЗТНЦФІ
Ј¬ЗТНЦФІ![]() ѕ№эµг
ѕ№эµг![]() .
.
ЈЁ1Ј©ЗуНЦФІ![]() µД±кЧј·ЅіМЈ»
µД±кЧј·ЅіМЈ»
ЈЁ2Ј©Иф№эЧуЅ№µг![]() ЗТЗгР±ЅЗОЄ45ЎгµДЦ±ПЯ
ЗТЗгР±ЅЗОЄ45ЎгµДЦ±ПЯ![]() УлНЦФІ
УлНЦФІ![]() Ѕ»УЪ
Ѕ»УЪ![]() БЅµгЈ¬ЗуПЯ¶О
БЅµгЈ¬ЗуПЯ¶О![]() µДі¤.
µДі¤.
Ійїґґр°ёєНЅвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com