
【题目】已知a>0,b>0,则“1![]() 2”是“a2+a=3b2+2b”的( )
2”是“a2+a=3b2+2b”的( )
A.充分不必要条件B.必要不充分条件
C.充分必要条件D.既不充分也不必要条件
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1的参数方程为![]() (
(![]() 为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C2:ρ2﹣4ρcosθ+3=0.
为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C2:ρ2﹣4ρcosθ+3=0.
(1)求曲线C1的一般方程和曲线C2的直角坐标方程;
(2)若点P在曲线C1上,点Q曲线C2上,求|PQ|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的正方形,
的正方形,![]() 是正三角形,
是正三角形,![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 为底面
为底面![]() 内的动点,则下列结论正确的是( )
内的动点,则下列结论正确的是( )

A.若![]() 时,平面
时,平面![]() 平面
平面![]()
B.若![]() 时,直线
时,直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]()
C.若直线![]() 和
和![]() 异面时,点
异面时,点![]() 不可能为底面
不可能为底面![]() 的中心
的中心
D.若平面![]() 平面
平面![]() ,且点
,且点![]() 为底面
为底面![]() 的中心时,
的中心时,![]()
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知圆F1:(x+1)2 +y2= r2(1≤r≤3),圆F2:(x-1)2+y2= (4-r)2.
(1)证明:圆F1与圆F2有公共点,并求公共点的轨迹E的方程;
(2)已知点Q(m,0)(m<0),过点E斜率为k(k≠0)的直线与(Ⅰ)中轨迹E相交于M,N两点,记直线QM的斜率为k1,直线QN的斜率为k2,是否存在实数m使得k(k1+k2)为定值?若存在,求出m的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为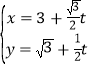 (
(![]() 为参数),点
为参数),点![]() 的极坐标为
的极坐标为![]() ,设直线
,设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在等腰![]() 中,
中,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() 为
为![]() 的中点,
的中点,![]() 在线段
在线段![]() 上,且
上,且![]() 。将
。将![]() 沿
沿![]() 折起,使点
折起,使点![]() 到
到![]() 的位置(如图2所示),且
的位置(如图2所示),且![]() 。
。
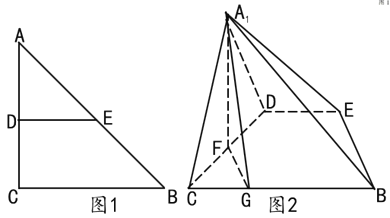
(1)证明:![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值
所成锐二面角的余弦值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“纹样”是中国艺术宝库的瑰宝,“火纹”是常见的一种传统纹样,为了测算某火纹纹样(如图阴影部分所示)的面积,作一个边长为3的正方形将其包含在内,并向该正方形内随机投掷2000个点,己知恰有800个点落在阴影部分,据此可估计阴影部分的面积是

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 的棱长均为2,O为AC的中点,平面A'OB⊥平面ABC,平面
的棱长均为2,O为AC的中点,平面A'OB⊥平面ABC,平面![]() ⊥平面ABC.
⊥平面ABC.
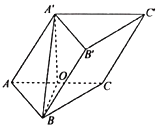
(1)求证:A'O⊥平面ABC;
(2)求二面角A﹣BC﹣C'的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com