
【题目】已知椭圆E:![]() 的焦点在x轴上,抛物线C:
的焦点在x轴上,抛物线C:![]() 与椭圆E交于A,B两点,直线AB过抛物线的焦点.
与椭圆E交于A,B两点,直线AB过抛物线的焦点.
(1)求椭圆E的方程和离心率e的值;
(2)已知过点H(2,0)的直线l与抛物线C交于M、N两点,又过M、N作抛物线C的切线l1,l2,使得l1⊥l2,问这样的直线l是否存在?若存在,求出直线l的方程;若不存在,说明理由.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)利用抛物线的方程求出点![]() 的坐标,代入椭圆的方程,即可求得
的坐标,代入椭圆的方程,即可求得![]() 的值,进而得到离心率的值;
的值,进而得到离心率的值;
(2)设直线![]() 的方程为
的方程为![]() ,由抛物线的方程得
,由抛物线的方程得![]() ,则
,则![]() ,所以切线
,所以切线![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,有题设条件得
,有题设条件得![]() ,再由直线的方程和抛物线的方程联立,利用韦达定理,得
,再由直线的方程和抛物线的方程联立,利用韦达定理,得![]() ,即可求得
,即可求得![]() ,得到直线的方程.
,得到直线的方程.
(1)∵x2=2py,∴![]() ,∴
,∴![]() 代入
代入![]() 得
得![]()
∴![]() 代点A到
代点A到![]() 得t=4.
得t=4.
∴椭圆E:![]() ,a=2,b=1,∴
,a=2,b=1,∴![]() ,∴离心率
,∴离心率![]() .
.
(2)依题意,直线l的斜率必存在,
设直线l的方程为y=k(x-2),M(x1,y1),N(x2,y2).
因为![]() 所以
所以![]()
所以切线l1,l2的斜率分别为![]() ,
,![]() .
.
当l1⊥l2时,![]() ,即x1x2=-2.
,即x1x2=-2.
由![]() 得
得![]() ,
,
所以![]() ,解得
,解得![]() .
.
又![]() 恒成立,
恒成立,
所以存在直线l的方程是![]() ,即
,即![]()


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
【题目】从1至9这9个自然数中任取两个:
![]() 恰有一个偶数和恰有一个奇数;
恰有一个偶数和恰有一个奇数;![]() 至少有一个是奇数和两个数都是奇数;
至少有一个是奇数和两个数都是奇数;
![]() 至多有一个奇数和两个数都是奇数;
至多有一个奇数和两个数都是奇数;![]() 至少有一个奇数和至少有一个偶数.
至少有一个奇数和至少有一个偶数.
在上述事件中,是对立事件的是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在直角坐标系![]() 中, 直线
中, 直线![]() 的参数方程为是
的参数方程为是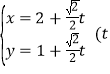 为参数), 以坐标原点
为参数), 以坐标原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系, 曲线
轴正半轴为极轴建立极坐标系, 曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1) 判断直线![]() 与曲线
与曲线![]() 的位置关系;
的位置关系;
(2) 在曲线![]() 上求一点
上求一点![]() ,使得它到直线
,使得它到直线![]() 的距离最大,并求出最大距离.
的距离最大,并求出最大距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个口袋中装有![]() 个红球
个红球![]() 且
且![]() 和
和![]() 个白球,一次摸奖从中摸两个球,两个球颜色不同则为中奖.
个白球,一次摸奖从中摸两个球,两个球颜色不同则为中奖.
(1)用![]() 表示一次摸奖中奖的概率
表示一次摸奖中奖的概率![]() ;
;
(2)若![]() ,设三次摸奖(每次摸奖后球放回)恰好有
,设三次摸奖(每次摸奖后球放回)恰好有![]() 次中奖,求
次中奖,求![]() 的数学期望
的数学期望![]() ;
;
(3)设三次摸奖(每次摸奖后球放回)恰好有一次中奖的概率![]() ,当
,当![]() 取何值时,
取何值时, ![]() 最大?
最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣1,g(x)=﹣x2+4x﹣3,若存在f(a)=g(b),则实数b的取值范围为( )
A.[1,3]
B.(1,3)
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某地区观众对大型综艺活动《中国好声音》的收视情况,随机抽取了100名观众进行调查,其中女性有55名.下面是根据调查结果绘制的观众收看该节目的场数与所对应的人数表:
场数 | 9 | 10 | 11 | 12 | 13 | 14 |
人数 | 10 | 18 | 22 | 25 | 20 | 5 |
将收看该节目场次不低于13场的观众称为“歌迷”,已知“歌迷”中有10名女性.
(1)根据已知条件完成下面的2×2列联表,并据此资料我们能否有95%的把握认为“歌迷”与性别有关?
非歌迷 | 歌迷 | 合计 | |
男 | |||
女 | |||
合计 |
(2)将收看该节目所有场次(14场)的观众称为“超级歌迷”,已知“超级歌迷”中有2名女性,若从“超级歌迷”中任意选取2人,求至少有1名女性观众的概率.
P(K2≥k) | 0.05 | 0.01 |
k | 3.841 | 6.635 |
附:K2=![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)
设函数![]() ,其中
,其中![]() .
.
( I )若函数![]() 图象恒过定点P,且点P在
图象恒过定点P,且点P在![]() 的图象上,求m的值;
的图象上,求m的值;
(Ⅱ)当![]() 时,设
时,设![]() ,讨论
,讨论![]() 的单调性;
的单调性;
(Ⅲ)在(I)的条件下,设![]() ,曲线
,曲线![]() 上是否存在两点P、Q,
上是否存在两点P、Q,
使△OPQ(O为原点)是以O为直角顶点的直角三角形,且该三角形斜边的中点在y轴上?如果存在,求a的取值范围;如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}是以d(d≠0)为公差的等差数列,a1=2,且a2 , a4 , a8成等比数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn=an2n(n∈N*),求数列{bn}的前n项和Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com