
| A.?α,β∈R,使cos(α+β)=cosα+sinβ |
| B.?a>0,函数f(x)=ln2x+lnx-a有零点 |
| C.?m∈R,使f(x)=(m-1)•xm2-4m+3是幂函数,且在(0,+∞)上递减 |
| D.?φ∈R,函数f(x)=sin(2x+φ)都不是偶函数 |
科目:高中数学 来源: 题型:
已知函数![]() 关于
关于![]() 的方程
的方程![]() ,下列四个命题中是假命题的是 ( )
,下列四个命题中是假命题的是 ( )
A.存在实数![]() ,使得方程恰有2个不同的实根;
,使得方程恰有2个不同的实根;
B.存在实数![]() ,使得方程恰有4个不同的实根;
,使得方程恰有4个不同的实根;
C.存在实数![]() ,使得方程恰有6个不同的实根;
,使得方程恰有6个不同的实根;
D.存在实数![]() ,使得方程恰有8个不同的实根;
,使得方程恰有8个不同的实根;
查看答案和解析>>
科目:高中数学 来源:2012届温州十校联合体高二第一学期期末联考数学试卷(理科) 题型:选择题
下列命题中是假命题的是 ( )
A.对于命题p:
B.抛物线y2 = 2x的焦点到准线的距离为1
C.“m= ”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0垂直”的充要条件
”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0垂直”的充要条件
D.直线与抛物线只有一个交点是直线与抛物线相切的必要不充分条件
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
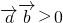 “是“
“是“ 的夹角为锐角”的充要条件
的夹角为锐角”的充要条件查看答案和解析>>
科目:高中数学 来源: 题型:单选题
 ”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0垂直”的充要条件
”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0垂直”的充要条件查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com