
ĄŸÌâÄżĄżÔÚłä·ÖŸșŐù”ÄÊĐłĄ»·ŸłÖĐŁŹČúÆ·”ĶšŒÛÖÁčŰÖŰÒȘŁŹËüœ«Ó°ÏìČúÆ·”ÄÏúÁżŁŹœű¶űÓ°ÏìÉúČúłÉ±ŸĄąÆ·ĆÆĐÎÏó”È![]() Äłč«ËŸžùŸĘ¶àÄê”ÄÊĐłĄŸŃ飏ŚÜœá”Ă”œÁËÆäÉúČú”ÄČúÆ·AÔÚÒ»žöÏúÊÛŒŸ¶È”ÄÏúÁż
Äłč«ËŸžùŸĘ¶àÄê”ÄÊĐłĄŸŃ飏ŚÜœá”Ă”œÁËÆäÉúČú”ÄČúÆ·AÔÚÒ»žöÏúÊÛŒŸ¶È”ÄÏúÁż![]() ”„λŁșÍòŒț
”„λŁșÍòŒț![]() ÓëÊÛŒÛ
ÓëÊÛŒÛ![]() ”„λŁșÔȘ
”„λŁșÔȘ![]() ÖźŒäÂúŚășŻÊęčŰÏ”
ÖźŒäÂúŚășŻÊęčŰÏ” ŁŹA”Ä”„ŒțłÉ±Ÿ
ŁŹA”Ä”„ŒțłÉ±Ÿ![]() ”„λŁșÔȘ
”„λŁșÔȘ![]() ÓëÏúÁżyÖźŒäÂúŚășŻÊęčŰÏ”
ÓëÏúÁżyÖźŒäÂúŚășŻÊęčŰÏ”![]() Łź
Łź
![]() ”±ČúÆ·A”ÄÊÛŒÛÔÚÊČĂŽ·¶Î§ÄÚʱŁŹÄÜÊč”ĂÆäÏúÁżČ»”ÍÓÚ5ÍòŒțŁż
”±ČúÆ·A”ÄÊÛŒÛÔÚÊČĂŽ·¶Î§ÄÚʱŁŹÄÜÊč”ĂÆäÏúÁżČ»”ÍÓÚ5ÍòŒțŁż
![]() ”±ČúÆ·A”ÄÊÛŒÛÎȘ¶àÉÙʱŁŹŚÜÀûÈóŚîŽóŁż
”±ČúÆ·A”ÄÊÛŒÛÎȘ¶àÉÙʱŁŹŚÜÀûÈóŚîŽóŁż![]() ŚąŁșŚÜÀûÈó
ŚąŁșŚÜÀûÈó![]() ÏúÁż
ÏúÁż![]() ÊÛŒÛ
ÊÛŒÛ![]() ”„ŒțłÉ±Ÿ
”„ŒțłÉ±Ÿ![]()
ĄŸŽđ°žĄżŁš1Ł©![]() Łš2Ł©14ÔȘ
Łš2Ł©14ÔȘ
ĄŸœâÎöĄż
Łš1Ł©žùŸĘÌâÖĐËùžű”ÄœâÎöÊœŁŹ·ÖÇéżöÁĐłöÆäÂúŚă”ÄČ»”ÈÊœŚéŁŹÇó”ĂœáčûŁ»
Łš2Ł©žùŸĘÌâÒ⣏ÁĐłöÀûÈó¶ÔÓŠ”ÄœâÎöÊœŁŹ·Ö¶ÎÇóŚîÖ”ŁŹŚîșó±ÈœÏÇó”Ăœáčû.
Łš1Ł©ÓÉ![]() ”ĂŁŹ
”ĂŁŹ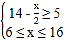 »ò
»ò![]()
œâ”ĂŁŹ![]() »ò
»ò![]() .
.
ŒŽ![]() .
.
ŽđŁș”±ČúÆ·A”ÄÊÛŒÛ![]() ʱŁŹÆäÏúÁżyČ»”ÍÓÚ5ÍòŒțĄŁ
ʱŁŹÆäÏúÁżyČ»”ÍÓÚ5ÍòŒțĄŁ
Łš2Ł©ÓÉÌâÒ⣏ŚÜÀûÈó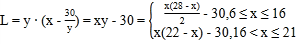
ąÙ”±![]() ʱŁŹ
ʱŁŹ![]() ŁŹ”±ÇÒœö”±
ŁŹ”±ÇÒœö”±![]() ʱ”ÈșĆłÉÁą.
ʱ”ÈșĆłÉÁą.
ąÚ”±![]() ʱŁŹ
ʱŁŹ![]() ”„”ś”ĘŒőŁŹ
”„”ś”ĘŒőŁŹ![]()
ËùÒÔŁŹ![]() ʱŁŹÀûÈó
ʱŁŹÀûÈó![]() ŚîŽó.
ŚîŽó.
ŽđŁș”±ČúÆ·A”ÄÊÛŒÛÎȘ14ÔȘʱŁŹŚÜÀûÈóŚîŽóĄŁ


 ŐăœĂûĐŁĂûÊŠœđŸíÏ”ÁĐŽđ°ž
ŐăœĂûĐŁĂûÊŠœđŸíÏ”ÁĐŽđ°ž
| Äꌶ | žßÖĐżÎłÌ | Äꌶ | łőÖĐżÎłÌ |
| žßÒ» | žßÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ | łőÒ» | łőÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ |
| žß¶ț | žß¶țĂâ·ŃżÎłÌÍÆŒöŁĄ | łő¶ț | łő¶țĂâ·ŃżÎłÌÍÆŒöŁĄ |
| žßÈę | žßÈęĂâ·ŃżÎłÌÍÆŒöŁĄ | łőÈę | łőÈęĂâ·ŃżÎłÌÍÆŒöŁĄ |
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÔÚĄśABCÖĐŁŹÒŃÖȘ”ăAŁš5ŁŹŁ2Ł©ŁŹBŁš7,3Ł©ŁŹÇÒ±ßAC”ÄÖĐ”ăMÔÚyÖáÉÏŁŹ±ßBC”ÄÖĐ”ăNÔÚxÖáÉÏŁŹÇóŁș
Łš1Ł©¶„”ăC”ÄŚű±êŁ»
Łš2Ł©Ö±ÏßMN”Ä·œłÌŁź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄż”±Ê”ÊęxŁŹyÂúŚă 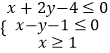 ʱŁŹ1ĄÜax+yĄÜ4șăłÉÁąŁŹÔòÊ”Êęa”ÄÈĄÖ”·¶Î§ÊÇ Łź
ʱŁŹ1ĄÜax+yĄÜ4șăłÉÁąŁŹÔòÊ”Êęa”ÄÈĄÖ”·¶Î§ÊÇ Łź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄż¶ÔÓÚșŻÊę![]() ŁŹÈôÔÚÆ䶚ÒćÓòÄÚŽæÔÚÊ”Êę
ŁŹÈôÔÚÆ䶚ÒćÓòÄÚŽæÔÚÊ”Êę![]() ŁŹÊč”Ă
ŁŹÊč”Ă![]() łÉÁąŁŹÔòłÆ
łÉÁąŁŹÔòłÆ![]() ÓĐĄ°Ąù”㥱
ÓĐĄ°Ąù”㥱![]() ĄŁ
ĄŁ
Łš1Ł©ĆжÏșŻÊę![]() ÔÚ
ÔÚ![]() ÉÏÊÇ·ńÓĐĄ°Ąù”㥱ĄŁČąË”ĂśÀíÓÉŁ»
ÉÏÊÇ·ńÓĐĄ°Ąù”㥱ĄŁČąË”ĂśÀíÓÉŁ»
Łš2Ł©ÈôșŻÊę![]() ÔÚ
ÔÚ![]() ÉÏÓĐĄ°Ąù”㥱ŁŹÇóŐęÊ”Êęa”ÄÈĄÖ”·¶Î§ĄŁ
ÉÏÓĐĄ°Ąù”㥱ŁŹÇóŐęÊ”Êęa”ÄÈĄÖ”·¶Î§ĄŁ
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÍščęËæ»úŃŻÎÊ100ĂûĐÔ±đȻ͏”Ğ߶țѧÉúÊÇ·ń°źłÔÁăÊłŁŹ”Ă”œÈçÏ”ÄÁĐÁȘ±íŁș
ÄĐ | Ćź | ŚÜŒÆ | |
°źșĂ | 10 | 40 | 50 |
Č»°źșĂ | 20 | 30 | 50 |
ŚÜŒÆ | 30 | 70 | 100 |
žœ±íŁș
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
ÆäÖĐ![]()
ÔòÏÂÁĐœáÂÛŐęÈ·”ÄÊÇŁš Ł©
A. ÔÚ·žŽíÎó”ÄžĆÂÊČ»łŹčę0.05”ÄÇ°ÌáÏÂŁŹÈÏÎȘĄ°ÊÇ·ń°źłÔÁăÊłÓëĐÔ±đÓĐčŰĄ±
B. ÔÚ·žŽíÎó”ÄžĆÂÊČ»łŹčę0.05”ÄÇ°ÌáÏÂŁŹÈÏÎȘĄ°ÊÇ·ń°źłÔÁăÊłÓëĐÔ±đÎȚčŰĄ±
C. ÔÚ·žŽíÎó”ÄžĆÂÊČ»łŹčę0.025”ÄÇ°ÌáÏÂŁŹÈÏÎȘĄ°ÊÇ·ń°źłÔÁăÊłÓëĐÔ±đÓĐčŰĄ±
D. ÔÚ·žŽíÎó”ÄžĆÂÊČ»łŹčę0.025”ÄÇ°ÌáÏÂŁŹÈÏÎȘĄ°ÊÇ·ń°źłÔÁăÊłÓëĐÔ±đÎȚčŰĄ±
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹÔÚËÄÀ⌶P©ABCDÖĐŁŹPAĄÍ”ŚĂæABCDŁŹADĄÍABŁŹABĄÎDCŁŹAD=DC=AP=2ŁŹAB=1ŁŹ”ăEÎȘÀâPC”ÄÖД㣟 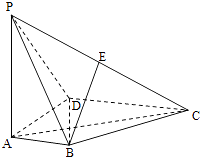
Łš1Ł©Ö€ĂśŁșBEĄÍDCŁ»
Łš2Ł©ÇóÖ±ÏßBEÓëÆœĂæPBDËùłÉœÇ”ÄŐęÏÒÖ”Ł»
Łš3Ł©ÈôFÎȘÀâPCÉÏÒ»”㣏ÂúŚăBFĄÍACŁŹÇó¶țĂæœÇF©AB©P”ÄÓàÏÒÖ”Łź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÏÂÁĐÎćžöœáÂÛŁș
![]() ŒŻșÏ
ŒŻșÏ![]() 2ŁŹ3ŁŹ4ŁŹ5ŁŹ
2ŁŹ3ŁŹ4ŁŹ5ŁŹ![]() ŁŹŒŻșÏ
ŁŹŒŻșÏ![]() ŁŹÈôfŁș
ŁŹÈôfŁș![]() ŁŹÔò¶ÔÓŠčŰÏ”fÊÇŽÓŒŻșÏA”œŒŻșÏB”ÄÓłÉ䣻
ŁŹÔò¶ÔÓŠčŰÏ”fÊÇŽÓŒŻșÏA”œŒŻșÏB”ÄÓłÉ䣻
![]() șŻÊę
șŻÊę![]() ”ĶšÒćÓòÎȘ
”ĶšÒćÓòÎȘ![]() ŁŹÔòșŻÊę
ŁŹÔòșŻÊę![]() ”ĶšÒćÓòÒČÊÇ
”ĶšÒćÓòÒČÊÇ![]() Ł»
Ł»
![]() ŽæÔÚÊ”Êę
ŽæÔÚÊ”Êę![]() ŁŹÊč”Ă
ŁŹÊč”Ă![]() łÉÁąŁ»
łÉÁąŁ»
![]() ÊÇșŻÊę
ÊÇșŻÊę![]() ”ĶԳÆÖá·œłÌŁ»
”ĶԳÆÖá·œłÌŁ»
![]() ÇúÏß
ÇúÏß![]() șÍÖ±Ïß
șÍÖ±Ïß![]() ”Äč«čČ”ăžöÊęÎȘmŁŹÔòmČ»żÉÄÜÎȘ1Ł»
”Äč«čČ”ăžöÊęÎȘmŁŹÔòmČ»żÉÄÜÎȘ1Ł»
ÆäÖĐŐęÈ·”ÄÓĐ______![]() ĐŽłöËùÓĐŐęÈ·”ÄĐòșĆ
ĐŽłöËùÓĐŐęÈ·”ÄĐòșĆ![]()
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÒŃÖȘșŻÊęfŁšxŁ©=sinŁš3x+ ![]() Ł©Łź
Ł©Łź
Łš1Ł©ÇófŁšxŁ©”Ä”„”ś”ĘÔöÇűŒäŁ»
Łš2Ł©ÈôŠÁÊǔڶțÏóÏȚœÇŁŹfŁš ![]() Ł©=
Ł©= ![]() cosŁšŠÁ+
cosŁšŠÁ+ ![]() Ł©cos2ŠÁŁŹÇócosŠÁ©sinŠÁ”ÄÖ”Łź
Ł©cos2ŠÁŁŹÇócosŠÁ©sinŠÁ”ÄÖ”Łź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄż(2015Ą€șț±±Ł©Äłł§ÓĂÏÊĆŁÄÌÔÚÄłÌšÉ豞ÉÏÉúČú![]() ÁœÖÖÄÌÖÆÆ·ŁźÉúČú1¶ÖAČúÆ·ĐèÏÊĆŁÄÌ2¶ÖŁŹÊčÓĂÉ豞1ĐĄÊ±ŁŹ»ńÀû1000ÔȘŁ»ÉúČú1¶ÖBČúÆ·ĐèÏÊĆŁÄÌ1.5¶ÖŁŹÊčÓĂÉ豞1.5ĐĄÊ±ŁŹ»ńÀû1200ÔȘŁźÒȘÇóĂżÌìBČúÆ·”ÄČúÁżČ»łŹčęAČúÆ·ČúÁż”Ä2±¶ŁŹÉè±žĂżÌìÉúČú
ÁœÖÖÄÌÖÆÆ·ŁźÉúČú1¶ÖAČúÆ·ĐèÏÊĆŁÄÌ2¶ÖŁŹÊčÓĂÉ豞1ĐĄÊ±ŁŹ»ńÀû1000ÔȘŁ»ÉúČú1¶ÖBČúÆ·ĐèÏÊĆŁÄÌ1.5¶ÖŁŹÊčÓĂÉ豞1.5ĐĄÊ±ŁŹ»ńÀû1200ÔȘŁźÒȘÇóĂżÌìBČúÆ·”ÄČúÁżČ»łŹčęAČúÆ·ČúÁż”Ä2±¶ŁŹÉè±žĂżÌìÉúČú![]() ÁœÖÖČúƷʱŒäÖźșÍČ»łŹčę12ĐĄÊ±. ŒÙ¶šĂżÌìżÉ»ńÈĄ”ÄÏÊĆŁÄÌÊęÁżWŁš”„λŁș¶ÖŁ©ÊÇÒ»žöËæ»ú±äÁżŁŹÆä·ÖČŒÁĐÎȘ
ÁœÖÖČúƷʱŒäÖźșÍČ»łŹčę12ĐĄÊ±. ŒÙ¶šĂżÌìżÉ»ńÈĄ”ÄÏÊĆŁÄÌÊęÁżWŁš”„λŁș¶ÖŁ©ÊÇÒ»žöËæ»ú±äÁżŁŹÆä·ÖČŒÁĐÎȘ
ŁšąńŁ©ÇóZ”Ä·ÖČŒÁĐșÍŸùÖ”Ł»žĂł§ĂżÌìžùŸĘ»ńÈĄ”ÄÏÊĆŁÄÌÊęÁż°ČĆĆÉúČúŁŹÊčÆä»ńÀûŚîŽóŁŹÒòŽËĂżÌì”ÄŚîŽó»ńÀûZŁš”„λŁșÔȘŁ©ÊÇÒ»žöËæ»ú±äÁżŁź
ŁšąòŁ© ÈôĂżÌìżÉ»ńÈĄ”ÄÏÊĆŁÄÌÊęÁżÏໄ¶ÀÁąŁŹÇó3ÌìÖĐÖÁÉÙÓĐ1Ìì”ÄŚîŽó»ńÀûłŹčę10000ÔȘ”ÄžĆÂÊŁź
Č鿎Žđ°žșÍœâÎö>>
°Ù¶ÈÖÂĐĆ - Á·Ï°ČáÁбí - ÊÔÌâÁбí
șț±±ÊĄ»„ÁȘÍű΄·šșÍČ»ÁŒĐĆÏąŸÙ±šÆœÌš | ÍűÉÏÓĐșŠĐĆÏąŸÙ±šŚšÇű | ”çĐĆŐ©ÆŸÙ±šŚšÇű | ÉæÀúÊ·ĐéÎȚÖśÒćÓĐșŠĐĆÏąŸÙ±šŚšÇű | ÉæÆóÇÖÈšŸÙ±šŚšÇű
΄·šșÍČ»ÁŒĐĆÏąŸÙ±š”ç»°Łș027-86699610 ŸÙ±šÓÊÏäŁș58377363@163.com