
°æƒø°ø±æ◊≈Ω°øµ°¢µÕúµƒ…˙ªÓ¿ÌƒÓ£¨◊‚”√π´π≤◊‘––≥µ∆Ô––µƒ»À‘Ω¿¥‘Ω∂ý£Æƒ≥÷÷π´π≤◊‘––≥µµƒ◊‚”√ ’∑—±Í◊ºŒ™£∫√ø¥Œ◊‚≥µ≤ª≥¨π˝1–° ±√‚∑—£¨≥¨π˝1–° ±µƒ≤ø∑÷√ø–° ± ’∑—2‘™(≤ª◊„1–° ±µƒ≤ø∑÷∞¥1–° ±º∆À„)£Æº◊°¢““¡Ω»Àœýª•∂¿¡¢¿¥◊‚≥µ£¨√ø»À∏˜◊‚1¡æ«“◊‚”√1¥Œ£Æ…˺◊°¢““≤ª≥¨π˝1–° ±ªπ≥µµƒ∏≈¬ ∑÷±Œ™![]() ∫Õ
∫Õ![]() £ª1–° ±“‘…œ«“≤ª≥¨π˝2–° ±ªπ≥µµƒ∏≈¬ ∑÷±Œ™
£ª1–° ±“‘…œ«“≤ª≥¨π˝2–° ±ªπ≥µµƒ∏≈¬ ∑÷±Œ™![]() ∫Õ
∫Õ![]() £ª¡Ω»À◊‚≥µ ±º‰∂º≤ªª·≥¨π˝3–° ±£Æ
£ª¡Ω»À◊‚≥µ ±º‰∂º≤ªª·≥¨π˝3–° ±£Æ
(1) «Ûº◊°¢““¡Ω»ÀÀ˘∏∂◊‚≥µ∑—”√œýÕ¨µƒ∏≈¬ £ª
(2) º«º◊°¢““¡Ω»ÀÀ˘∏∂µƒ◊‚≥µ∑—”√÷Æ∫ÕŒ™Àʪ˙±‰¡ø![]() £¨«Û
£¨«Û![]() µƒ∑÷≤º¡–∫Õ ˝—ß∆⁄Õ˚
µƒ∑÷≤º¡–∫Õ ˝—ß∆⁄Õ˚![]() £Æ
£Æ
°æ¥∞∏°ø£®1£©![]() £®2£©∑÷≤º¡–º˚Ω‚Œˆ£¨
£®2£©∑÷≤º¡–º˚Ω‚Œˆ£¨![]()
°æΩ‚Œˆ°ø
£®1£©∏˘æð“‚£¨¿˚”√œýª•∂¿¡¢ ¬º˛µƒ∏≈¬ π´ Ωº∆À„ø…µ√.
£®2£©”…“‚![]() µƒø…ƒÐ»°÷µŒ™0£¨2£¨4£¨6£¨8£¨∑÷±«Û≥ˆœý”¶µƒ∏≈¬ £¨”…¥ÀƒÐ«Û≥ˆ
µƒø…ƒÐ»°÷µŒ™0£¨2£¨4£¨6£¨8£¨∑÷±«Û≥ˆœý”¶µƒ∏≈¬ £¨”…¥ÀƒÐ«Û≥ˆ![]() µƒ∑÷≤º¡–º∞ ˝—ß∆⁄Õ˚£Æ
µƒ∑÷≤º¡–º∞ ˝—ß∆⁄Õ˚£Æ
Ω‚£∫£®1£©”…”⁄¡Ω»À◊‚≥µ ±º‰∂º≤ªª·≥¨π˝3–° ±£¨
∏˘æð“‚£¨√ø»ÀÀ˘∏∂∑—”√ø…ƒÐŒ™![]() £¨
£¨![]() £¨
£¨![]() ‘™£Æ
‘™£Æ
“Ú¥À£¨¡Ω»À∂º∏∂![]() ‘™µƒ∏≈¬ Œ™
‘™µƒ∏≈¬ Œ™![]() £¨
£¨
∂º∏∂2‘™µƒ∏≈¬ Œ™![]() £¨
£¨
∂º∏∂4‘™µƒ∏≈¬ Œ™![]() .
.
À˘“‘£¨¡Ω»ÀÀ˘∏∂∑—”√œýÕ¨µƒ∏≈¬ Œ™![]()
£®2£©∏˘æð“‚£¨”…“—÷™µ√![]() µƒø…ƒÐ»°÷µŒ™0£¨2£¨4£¨6£¨8£¨
µƒø…ƒÐ»°÷µŒ™0£¨2£¨4£¨6£¨8£¨
![]() £¨
£¨
![]() £¨
£¨
![]() £¨
£¨
![]() £¨
£¨
![]() £¨
£¨
![]() µƒ∑÷≤º¡–Œ™£∫
µƒ∑÷≤º¡–Œ™£∫
| 0 | 2 | 4 | 6 | 8 |
|
|
|
|
|
|
![]() £Æ
£Æ


 “ªæÌ∏„∂®œµ¡–¥∞∏
“ªæÌ∏„∂®œµ¡–¥∞∏ √˚–£◊˜“µ±æœµ¡–¥∞∏
√˚–£◊˜“µ±æœµ¡–¥∞∏ «·«…∂·π⁄÷Ð≤‚‘¬øº÷±Õ®√˚–£œµ¡–¥∞∏
«·«…∂·π⁄÷Ð≤‚‘¬øº÷±Õ®√˚–£œµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øº∆ªÆ‘⁄ƒ≥ÀÆø‚Ω®“ª◊˘÷¡∂ý∞≤◊∞3î∑¢µÁª˙µƒÀƵÁ’æ£¨π˝»•50ƒÍµƒÀÆŒƒ◊ ¡œœ‘ 棨ÀÆø‚ƒÍ»Î¡˜¡ø![]() (ƒÍ»Î¡˜¡ø£∫“ªƒÍƒ⁄…œ”Œ¿¥ÀÆ”Îø‚«¯ΩµÀÆ÷Æ∫Õ.µ•Œª£∫“⁄¡¢∑Ω√◊£©∂º‘⁄40“‘…œ.∆‰÷–£¨≤ª◊„80µƒƒÍ∑ð”–10ƒÍ£¨≤ªµÕ”⁄80«“≤ª≥¨π˝120µƒƒÍ∑ð”–35ƒÍ£¨≥¨π˝120µƒƒÍ∑ð”–5ƒÍ.Ω´ƒÍ»Î¡˜¡ø‘⁄“‘…œ»˝∂Œµƒ∆µ¬ ◊˜Œ™œý”¶∂Œµƒ∏≈¬ £¨≤¢ºŸ…Ë∏˜ƒÍµƒƒÍ»Î¡˜¡øœýª•∂¿¡¢.
(ƒÍ»Î¡˜¡ø£∫“ªƒÍƒ⁄…œ”Œ¿¥ÀÆ”Îø‚«¯ΩµÀÆ÷Æ∫Õ.µ•Œª£∫“⁄¡¢∑Ω√◊£©∂º‘⁄40“‘…œ.∆‰÷–£¨≤ª◊„80µƒƒÍ∑ð”–10ƒÍ£¨≤ªµÕ”⁄80«“≤ª≥¨π˝120µƒƒÍ∑ð”–35ƒÍ£¨≥¨π˝120µƒƒÍ∑ð”–5ƒÍ.Ω´ƒÍ»Î¡˜¡ø‘⁄“‘…œ»˝∂Œµƒ∆µ¬ ◊˜Œ™œý”¶∂Œµƒ∏≈¬ £¨≤¢ºŸ…Ë∏˜ƒÍµƒƒÍ»Î¡˜¡øœýª•∂¿¡¢.
£®1£©«ÛŒ¥¿¥4ƒÍ÷–£¨÷¡∂ý1ƒÍµƒƒÍ»Î¡˜¡ø≥¨π˝120µƒ∏≈¬ £ª
£®2£©ÀƵÁ’朣Õ˚∞≤◊∞µƒ∑¢µÁª˙æ°ø…ƒÐ‘À––£¨µ´√øƒÍ∑¢µÁª˙◊Ó∂ýø…‘À––î ˝ ЃͻΡ˜¡ø![]() œÞ÷∆£¨≤¢”–»Áœ¬πÿœµ:
œÞ÷∆£¨≤¢”–»Áœ¬πÿœµ:
ƒÍ»Î¡˜¡ø |
|
|
|
∑¢µÁ¡ø◊Ó∂ýø…‘À––î ˝ | 1 | 2 | 3 |
»Ùƒ≥î∑¢µÁª˙‘À––£¨‘Ú∏√îƒÍ¿˚»ÛŒ™5000ÕÚ‘™£ª»Ùƒ≥î∑¢µÁª˙Œ¥‘À––£¨‘Ú∏√îƒÍø˜À800ÕÚ‘™£¨”˚ πÀƵÁ’æƒÍ◊п˚»Ûµƒæ˘÷µ¥ÔµΩ◊Ó¥Û£¨”¶∞≤◊∞∑¢µÁª˙∂ý…ŸÃ®£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“‘∆Ω√Ê÷±Ω«◊¯±Íœµµƒ‘≠µ„Œ™º´µ„£¨x÷·µƒ’˝∞Î÷·Œ™º´÷·Ω®¡¢º´◊¯±Íœµ.
£®1£© ‘∑÷±Ω´«˙œþC1µƒº´◊¯±Í∑Ω≥ö—£Ωsin¶»£≠cos¶»∫Õ«˙œþC2µƒ≤Œ ˝∑Ω≥Ã![]() £®tŒ™≤Œ ˝£©ªØŒ™÷±Ω«◊¯±Í∑Ω≥Ã∫Õ∆’Õ®∑Ω≥ãª
£®tŒ™≤Œ ˝£©ªØŒ™÷±Ω«◊¯±Í∑Ω≥Ã∫Õ∆’Õ®∑Ω≥ãª
£®2£©»Ù∫Ϭϓœ∫Õ∫⁄¬Ï“œ∑÷±‘⁄«˙œþC1∫Õ«˙œþC2…œ≈¿––£¨«Û∫Ϭϓœ∫Õ∫⁄¬Ï“œ÷ƺ‰µƒ◊Ó¥Ûæý¿Î£® ”¬Ï“œŒ™µ„£©.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝![]() £®
£®![]() £¨
£¨![]() «◊‘»ª∂‘ ˝µƒµ◊ ˝£©
«◊‘»ª∂‘ ˝µƒµ◊ ˝£©
(¢Ò) …Ë![]() £®∆‰÷–
£®∆‰÷–![]() «
«![]() µƒµº ˝£©£¨«Û
µƒµº ˝£©£¨«Û![]() µƒº´–°÷µ£ª
µƒº´–°÷µ£ª
(¢Ú) »Ù∂‘![]() £¨∂º”–
£¨∂º”–![]() ≥…¡¢£¨«Û µ ˝
≥…¡¢£¨«Û µ ˝![]() µƒ»°÷µ∑∂Œß.
µƒ»°÷µ∑∂Œß.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝![]() «°”–¡Ω∏ˆº´÷µµ„
«°”–¡Ω∏ˆº´÷µµ„![]() .
.
(1)«Û µ ˝![]() µƒ»°÷µ∑∂Œß£ª
µƒ»°÷µ∑∂Œß£ª
(2)«Û÷§£∫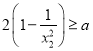 £ª
£ª
(3)«Û÷§£∫ ![]() £®∆‰÷–
£®∆‰÷–![]() Œ™◊‘»ª∂‘ ˝µƒµ◊ ˝£©.
Œ™◊‘»ª∂‘ ˝µƒµ◊ ˝£©.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø¥”≈˙¡øΩœ¥Ûµƒ≤˙∆∑÷–Àʪ˙»°≥ˆ10º˛≤˙∆∑Ω¯––÷ ¡øºÏ≤‚£¨»Ù’‚≈˙≤˙∆∑µƒ≤ª∫œ∏Ò¬ Œ™0.05£¨Àʪ˙±‰¡ø![]() ±Ì æ’‚10º˛≤˙∆∑÷–µƒ≤ª∫œ∏Ò≤˙∆∑µƒº˛ ˝£Æ
±Ì æ’‚10º˛≤˙∆∑÷–µƒ≤ª∫œ∏Ò≤˙∆∑µƒº˛ ˝£Æ
£®1£©Œ £∫’‚10º˛≤˙∆∑÷–°∞«°∫√”–2º˛≤ª∫œ∏Òµƒ∏≈¬ ![]() °±∫Õ°∞«°∫√”–3º˛≤ª∫œ∏Òµƒ∏≈¬
°±∫Õ°∞«°∫√”–3º˛≤ª∫œ∏Òµƒ∏≈¬ ![]() °±ƒƒ∏ˆ¥Û£ø«ÎÀµ√˜¿Ì”…£ª
°±ƒƒ∏ˆ¥Û£ø«ÎÀµ√˜¿Ì”…£ª
£®2£©«ÛÀʪ˙±‰¡ø![]() µƒ ˝—ß∆⁄Õ˚
µƒ ˝—ß∆⁄Õ˚![]() £Æ
£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™’˝Àƒ¿‚◊∂![]() µƒ≤ý¿‚∫Õµ◊√ʱþ≥§œýµ»£¨‘⁄’‚∏ˆ’˝Àƒ¿‚◊∂µƒ
µƒ≤ý¿‚∫Õµ◊√ʱþ≥§œýµ»£¨‘⁄’‚∏ˆ’˝Àƒ¿‚◊∂µƒ![]() Ãı¿‚÷–»Œ»°¡ΩÃı£¨∞¥œ¬¡–∑Ω Ω∂®“ÂÀʪ˙±‰¡ø
Ãı¿‚÷–»Œ»°¡ΩÃı£¨∞¥œ¬¡–∑Ω Ω∂®“ÂÀʪ˙±‰¡ø![]() µƒ÷µ£∫
µƒ÷µ£∫
»Ù’‚¡ΩÃı¿‚À˘‘⁄µƒ÷±œþœýΩª£¨‘Ú![]() µƒ÷µ «’‚¡ΩÃı¿‚À˘‘⁄÷±œþµƒº–Ω«¥Û–°£®ª°∂»÷∆£©£ª
µƒ÷µ «’‚¡ΩÃı¿‚À˘‘⁄÷±œþµƒº–Ω«¥Û–°£®ª°∂»÷∆£©£ª
»Ù’‚¡ΩÃı¿‚À˘‘⁄µƒ÷±œþ∆Ω––£¨‘Ú![]() £ª
£ª
»Ù’‚¡ΩÃı¿‚À˘‘⁄µƒ÷±œþ“Ï√Ê£¨‘Ú![]() µƒ÷µ «’‚¡ΩÃı¿‚À˘‘⁄÷±œþÀ˘≥…Ω«µƒ¥Û–°(ª°∂»÷∆).
µƒ÷µ «’‚¡ΩÃı¿‚À˘‘⁄÷±œþÀ˘≥…Ω«µƒ¥Û–°(ª°∂»÷∆).
£®1£©«Û![]() µƒ÷µ£ª
µƒ÷µ£ª
£®2£©«ÛÀʪ˙±‰¡ø![]() µƒ∑÷≤º¡–º∞ ˝—ß∆⁄Õ˚
µƒ∑÷≤º¡–º∞ ˝—ß∆⁄Õ˚![]() .
.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™a£æ0£¨∫Ø ˝f£®x£©£Ω|2x+2|+|x©Åa|µƒ◊Ó–°÷µŒ™2£Æ

£®1£©«Û µ ˝aµƒ÷µ£¨≤¢◊˜≥ˆy£Ωf£®x£©µƒÕºœÛ£ª
£®2£©µ±m£æ0£¨n£æ0£¨«“m+n£Ω2![]() ±£¨m2+n2°ðf£®x£©∫„≥…¡¢£¨«Û µ ˝xµƒ»°÷µ∑∂Œß£Æ
±£¨m2+n2°ðf£®x£©∫„≥…¡¢£¨«Û µ ˝xµƒ»°÷µ∑∂Œß£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com