
【题目】已知椭圆![]() 的离心率
的离心率![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,点
,点![]() ,点
,点![]() 在线段
在线段![]() 的中垂线上.
的中垂线上.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,直线
两点,直线![]() 与
与![]() 的倾斜角分别为
的倾斜角分别为![]() ,且
,且![]() ,求证:直线
,求证:直线![]() 过定点,并求该定点的坐标.
过定点,并求该定点的坐标.
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和是Sn , 若点An(n, ![]() )在函数f(x)=﹣x+c的图象上运动,其中c是与x无关的常数,且a1=3(n∈N*).
)在函数f(x)=﹣x+c的图象上运动,其中c是与x无关的常数,且a1=3(n∈N*).
(1)求数列{an}的通项公式;
(2)记bn=a ![]() ,求数列{bn}的前n项和Tn的最小值.
,求数列{bn}的前n项和Tn的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在
是定义在![]() 上的偶函数,且当
上的偶函数,且当![]() 时,
时,![]() .
.

(1)已画出函数![]() 在
在![]() 轴左侧的图像,如图所示,请补出完整函数
轴左侧的图像,如图所示,请补出完整函数![]() 的图像,并根据图像写出函数
的图像,并根据图像写出函数![]() 的增区间;
的增区间;
⑵写出函数![]() 的解析式和值域.
的解析式和值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于区间![]() ,若函数
,若函数![]() 同时满足:①
同时满足:①![]() 在
在![]() 上是单调函数;②函数
上是单调函数;②函数![]() ,
,![]() 的值域是
的值域是![]() ,则称区间
,则称区间![]() 为函数
为函数![]() 的“保值”区间.
的“保值”区间.
(1)求函数![]() 的所有“保值”区间.
的所有“保值”区间.
(2)函数![]() 是否存在“保值”区间?若存在,求出
是否存在“保值”区间?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将两块三角板按图甲方式拼好,其中![]() ,
, ![]() ,
, ![]() ,
,
![]() ,现将三角板
,现将三角板![]() 沿
沿![]() 折起,使
折起,使![]() 在平面
在平面![]() 上的射影
上的射影![]() 恰好在
恰好在![]() 上,如图乙.
上,如图乙.
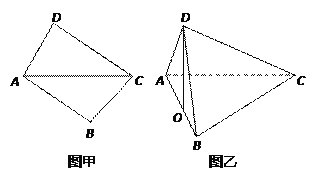
(1)求证: ![]() ;
;
(2)求证: ![]() 为线段
为线段![]() 中点;
中点;
(3)求二面角![]() 的大小的正弦值.
的大小的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x﹣2|﹣|2x+l|.
(I)求不等式f(x)≤x的解集;
(II )若不等式f(x)≥t2﹣t在x∈[﹣2,﹣1]时恒成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(
=( ![]() sinx,﹣1),
sinx,﹣1), ![]() =(cosx,m),m∈R.
=(cosx,m),m∈R.
(1)若m= ![]() ,且
,且 ![]() ∥
∥ ![]() ,求
,求 ![]() 的值;
的值;
(2)已知函数f(x)=2( ![]() +
+ ![]() )
) ![]() ﹣2m2﹣1,若函数f(x)在[0,
﹣2m2﹣1,若函数f(x)在[0, ![]() ]上有零点,求m的取值范围.
]上有零点,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海安市江淮文化园是以江淮历史文化为底蕴的人文景观,整个园区由白龙故里、先贤景区、凤山书院、中国名人艺术馆群四大景区组成.据估计,其中凤山书院景区每天的水电、人工等固定成本为1000元,另每增加一名游客需另外增加成本10元,凤山书院景区门票单价x(元)(x∈N*)与日门票销售量![]() (张)的关系如下表,并保证凤山书院景区每天盈利.
(张)的关系如下表,并保证凤山书院景区每天盈利.
x | 20 | 35 | 40 | 50 |
y | 400 | 250 | 200 | 100 |
(1)在坐标图纸中,根据表中提供的数据,描出实数对![]() 的对应点,并确定y与x的函数关系式;
的对应点,并确定y与x的函数关系式;
(2)求出![]() 的值,并解释其实际意义;
的值,并解释其实际意义;
(3)请写出凤山书院景区的日利润![]() 的表达式,并回答该景区怎样定价才能获最大日利润?
的表达式,并回答该景区怎样定价才能获最大日利润?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com