
���� ��1�����ֱ�ߵ���ͨ���̣��ɴ������ֱ�ߵ���б�ǣ�
��2���ٵ�sin��=0ʱ�����̱�ʾһ��ֱ�ߣ���y���cos��=0ʱ����ʾx���ϵ��������ߣ���sin�ȡ�0����cos�ȡ�0ʱ����ʾ˫���ߣ�
��t�١�1ʱ����ʾ������x���ϵ���Բ����t=1ʱ����ʾx���ϵ�һ���߶Σ�
��3���ȰѲ������̻�����ͨ���̣��ɴ�����������
��� �⣺��1����ֱ��$\left\{\begin{array}{l}{x=-2+tcos30��}\\{y=3-tsin60��}\end{array}\right.$��tΪ��������
����ȥ����t����ֱ�ߵ���ͨ����Ϊ��x+y-1=0��
��ֱ�ߵ�б��k=-1����ֱ�ߵ���б��Ϊ135�㣮
�ʴ�Ϊ��135�㣮
��2���١߲�������$\left\{\begin{array}{l}{x=��t+\frac{1}{t}��sin��}\\{y=��t-\frac{1}{t}��cos��}\end{array}\right.$��t��0����tΪ������
�൱sin��=0ʱ�����̱�ʾһ��ֱ�ߣ���y���cos��=0ʱ����ʾx���ϵ��������ߣ�
��sin�ȡ�0����cos�ȡ�0ʱ���Ѳ������̻�Ϊ��ͨ���̣��ã�
$\frac{{x}^{2}}{si{n}^{2}��}+\frac{{y}^{2}}{co{s}^{2}��}$=2��${t}^{2}+\frac{1}{{t}^{2}}$������ʾ˫���ߣ�
�ڡ߲�������$\left\{\begin{array}{l}{x=��t+\frac{1}{t}��sin��}\\{y=��t-\frac{1}{t}��cos��}\end{array}\right.$��t��0������Ϊ������
��t�١�1ʱ��$\frac{{x}^{2}}{��t+\frac{1}{t}��^{2}}$+$\frac{{y}^{2}}{��t-\frac{1}{t}��^{2}}$=1����ʾ������x���ϵ���Բ��
��t=1ʱ����ʾx���ϵ�һ���߶Σ�
��3����������$\left\{\begin{array}{l}{x=sin��}\\{y=3sin��}\end{array}\right.$����Ϊ������������ͨ���̵ã�${x}^{2}+\frac{{y}^{2}}{3}=1$��
��ʾ������y���ϵ���Բ��
���� ���⿼��ֱ�ߵ���б�ǵ�������������״���жϣ����е��⣬����ʱҪ�������⣬ע��������̺���ͨ���̵ĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
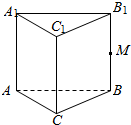 ��ͼ��ʾ����������ABC-A1B1C1�У�M��BB1���е㣬�������и�ʽ������ͼ�б������õ���������
��ͼ��ʾ����������ABC-A1B1C1�У�M��BB1���е㣬�������и�ʽ������ͼ�б������õ����������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-1��3�� | B�� | ��-�ޣ�-1���ȣ�3��+�ޣ� | C�� | [-3��1] | D�� | ��-�ޣ�-1]��[3��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com