
【题目】如图,在多面体![]() 中,
中,![]() 两两垂直,四边形
两两垂直,四边形![]() 是边长为2的正方形,
是边长为2的正方形,![]() ,
,![]() ,且
,且![]() ,
,![]() .
.
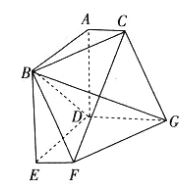
(1)证明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)连接AE,EG,根据直线的垂直关系可得![]() 平面
平面![]() 及
及![]() 平面
平面![]() ,结合所给边长及平行关系可知四边形
,结合所给边长及平行关系可知四边形![]() 是菱形,进而得到
是菱形,进而得到![]() ,在正方形
,在正方形![]() 中
中![]() 平面
平面![]() 。
。
(2)建立空间直角坐标系,写出各个点的坐标,求得平面![]() 的法向量
的法向量![]() 及平面
及平面![]() 的法向量
的法向量![]() ,即可利用向量的数量积关系求得二面角
,即可利用向量的数量积关系求得二面角![]() 的余弦值。
的余弦值。
(1)证明:连接![]() ,
,
因为![]() 两两垂直,所以
两两垂直,所以![]() 平面
平面![]()
因为![]() ,所以
,所以![]() ,又
,又![]() ,所以
,所以![]() 平面
平面![]()
所以![]() ,又因为
,又因为![]() ,所以四边形
,所以四边形![]() 是菱形,所以
是菱形,所以![]()
易知四边形![]() 是平行四边形,所以
是平行四边形,所以![]()
在正方形![]() 中,
中,![]() ,故
,故![]()
又![]() ,所以
,所以![]() 平面
平面![]()
(2)由(1)知![]() 两两互相垂直,故以
两两互相垂直,故以![]() 为坐标原点,以
为坐标原点,以![]() 所在直线为
所在直线为![]() 轴建立如图所示的空间直角坐标系
轴建立如图所示的空间直角坐标系![]() ,
,
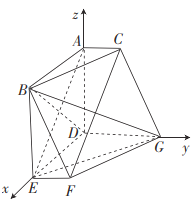
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
设![]() 为平面
为平面![]() 的法向量,
的法向量,
则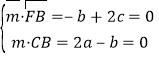
令![]() ,则
,则![]() ,
,![]() ,所以
,所以![]()
又因为![]() 平面
平面![]() ,所以
,所以![]() 为平面
为平面![]() 的一个法向量
的一个法向量
![]()
由图可知二面角![]() 是钝角,所以二面角
是钝角,所以二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】甲乙两人进行围棋比赛,约定先连胜两局者直接赢得比赛,若赛完5局仍未出现连胜,则判定获胜局数多者赢得比赛,假设每局甲获胜的概率为![]() ,乙获胜的概率为
,乙获胜的概率为![]() ,各局比赛结果相互独立.
,各局比赛结果相互独立.
求甲在4局以内(含4局)赢得比赛的概率;
记![]() 为比赛决出胜负时的总局数,求
为比赛决出胜负时的总局数,求![]() 的分布列和均值(数学期望).
的分布列和均值(数学期望).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】首届中国国际进口博览会期间,甲、乙、丙三家中国企业都有意向购买同一种型号的机床设备,他们购买该机床设备的概率分别为![]() ,且三家企业的购买结果相互之间没有影响,则三家企业中恰有1家购买该机床设备的概率是
,且三家企业的购买结果相互之间没有影响,则三家企业中恰有1家购买该机床设备的概率是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求函数的极值;
垂直,求函数的极值;
(2)设函数![]() .当
.当![]() =
=![]() 时,若区间[1,e]上存在x0,使得
时,若区间[1,e]上存在x0,使得![]() ,求实数
,求实数![]() 的取值范围.(
的取值范围.(![]() 为自然对数底数)
为自然对数底数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国上是世界严重缺水的国家,城市缺水问题较为突出,某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准![]() (吨),用水量不超过
(吨),用水量不超过![]() 的部分按平价收费,超过
的部分按平价收费,超过![]() 的部分按议价收费,为了了解全市民月用水量的分布情况,通过抽样,获得了100位居民某年的月用水量(单位:吨),将数据按照
的部分按议价收费,为了了解全市民月用水量的分布情况,通过抽样,获得了100位居民某年的月用水量(单位:吨),将数据按照![]() ,
, ![]() ,…,
,…, ![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.

(Ⅰ)求直方图中![]() 的值;
的值;
(Ⅱ)已知该市有80万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(Ⅲ)若该市政府希望使![]() 的居民每月的用水量不超过标准
的居民每月的用水量不超过标准![]() (吨),估计
(吨),估计![]() 的值,并说明理由;
的值,并说明理由;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC—A1B1C1中,BC=3,AB=4,AC=CC1=5,M,N分别是A1B,B1C1的中点.
(1)求证:MN//平面ACC1A1;
(2)求点N到平面MBC的距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com