
| 2500 |
| x |
| 2500 |
| x |
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省汕尾市陆丰市启恩中学高三数学专题练习:不等式(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省汕头市高三毕业班教学质量检测文科数学(含解析) 题型:解答题
(本题满分12分)
某商店经销一种洗衣粉,年销售总量为6000包,每包进价为2.8元,销售价为3.4元,全年分若干次进货,每次进货均为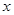 包,已知每次进货的运输劳务费为62.5元,全部洗衣粉一年的保管费为1.5
包,已知每次进货的运输劳务费为62.5元,全部洗衣粉一年的保管费为1.5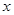 元.
元.
(1)将该商店经销洗衣粉一年的利润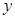 (元)表示为每次进货量
(元)表示为每次进货量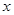 (包)的函数;
(包)的函数;
(2)为使利润最大,每次应进货多少包?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com