
����Ŀ��ij����Ϊ�˶����з���һ�ֲ�Ʒ���к������ۣ����ò�Ʒ�������ⶩ�ļ۸���������õ��������ݣ�
����x��Ԫ�� | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
����y������ | 92 | 82 | 83 | 80 | 75 | 68 |
��1�����y����x�����Իع鷽�� ![]() ������
������ ![]() =250
=250
��2��Ԥ���ڽ��������У������뵥����Ȼ���ӣ�I���еĹ�ϵ���Ҹò�Ʒ�ijɱ���4Ԫÿ����Ϊʹ�������������ò�Ʒ�ĵ���Ӧ��Ϊ����Ԫ��
���𰸡�
��1���⣺���� ![]() =
= ![]() ��8+8.2+8.4+8.6+8.8+9��=8.5
��8+8.2+8.4+8.6+8.8+9��=8.5
![]() =
= ![]() ��90+84+83+80+75+68��=80��
��90+84+83+80+75+68��=80��
���뷽�̿ɵã�80=8.5b+250���ɵ�b=��20
���ԴӶ��ع�ֱ�߷���Ϊy=��20x+250
��2���⣺�蹤����õ�����ΪLԪ���������
L=x����20x+250����4����20x+250��
=��20x2+330x��1000
=��20��x��8.25��2+361.25��
���ҽ���x=8.25ʱ��Lȡ�����ֵ��
�ʵ����۶�Ϊ8.25Ԫʱ�������ɻ���������
����������1������ƽ���������� ![]() =250�����b��������ûع�ֱ�߷��̣���2���蹤����õ�����ΪLԪ����������=�������멁�ɱ������������������䷽��������õ��������
=250�����b��������ûع�ֱ�߷��̣���2���蹤����õ�����ΪLԪ����������=�������멁�ɱ������������������䷽��������õ��������


 һŵ��ҵ�����ҵ���ּ�����������������ϵ�д�
һŵ��ҵ�����ҵ���ּ�����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ʽ|x��3|+|x��4|��2a��
��1����a=1����ʽ�Ľ⼯��
��2������֪����ʽ�н⣬��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ⳤΪ1��������ABCD��A1B1C1D1�У�E��BC���е㣬F����CD�ϵĶ��㣬GΪC1D1���е㣬HΪA1G���е㣮 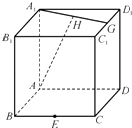
��1������F���D�غ�ʱ����֤��EF��AH��
��2��������C1��EF��C�Ĵ�СΪ�ȣ���ȷ����F��λ�ã�ʹ��sin ��= ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������Ϊ��0��+�ޣ��ĺ���f��x�����㣺
��x��1ʱ��f��x����0��
��f�� ![]() ��=1��
��=1��
�۶��������ʵ��x��y������f��xy��=f��x��+f��y����
��1����֤��f�� ![]() ��=��f��x����
��=��f��x����
��2����֤��f��x���ڶ�������Ϊ��������
��3�������㲻��ʽf��log0.5m+3��+f��2log0.5m��1���ݩ�2��m���ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��= ![]() �����г���a��0����a��1����
�������a��0����a��1����
��1����a=10ʱ�������x�ķ���f��x��=m�����г���m��2 ![]() ����
����
��2��������f��x���ڣ����ޣ�2]�ϵ���Сֵ��һ����a�صij�������ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=x2+bx+c����f��2��x��=f��2+x����f��0����0����f��m��=f��n��=0��m��n������log4m�� ![]() n��ֵ�ǣ� ��
n��ֵ�ǣ� ��
A.��1
B.����1
C.����1
D.��b�ķ���ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=x��1+ ![]() ����a��R��eΪ��Ȼ�����ĵ�������
����a��R��eΪ��Ȼ�����ĵ�������
��1������f��x���ĵ������䣻
��2����a=1ʱ����ֱ��l��y=kx��1������y=f��x��û�й����㣬��k�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֵ
��1����֪f��3x��=xlg9����f��2��+f��5����ֵ��
��2����3a=5b=A��ab��0������ ![]() =2����A��ֵ��
=2����A��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڼ�����![]() �У��ı���
�У��ı���![]() �Ǿ��Σ�
�Ǿ��Σ� ![]() ƽ��
ƽ��![]() ��
�� ![]() .
. ![]() ��
�� ![]() �ֱ����߶�
�ֱ����߶�![]() ���е�.
���е�.
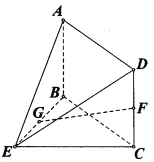
������֤�� ![]() ƽ��
ƽ��![]() ��
��
������![]() ��ƽ��
��ƽ��![]() ���ɽǵ�����ֵ.
���ɽǵ�����ֵ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com