
【题目】【2017广东佛山二模】已知椭圆![]() :
: ![]() (
(![]() )的焦距为4,左、右焦点分别为
)的焦距为4,左、右焦点分别为![]() 、
、![]() ,且
,且![]() 与抛物线
与抛物线![]() :
: ![]() 的交点所在的直线经过
的交点所在的直线经过![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
, ![]() 两点,与抛物线
两点,与抛物线![]() 无公共点,求
无公共点,求![]() 的面积的取值范围.
的面积的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)  .
.
【解析】试题分析:(1)先根据焦距确定焦点坐标,再根据对称性得![]() 与抛物线
与抛物线![]() :
: ![]() 的交点所在的直线为
的交点所在的直线为![]() ,即得一个交点为
,即得一个交点为![]() ,代入椭圆方程,结合
,代入椭圆方程,结合![]() 可解得
可解得![]() ,
, ![]() ;(2)先设直线
;(2)先设直线![]() :
: ![]() ,由直线
,由直线![]() 与抛物线
与抛物线![]() 无公共点,利用判别式小于零得
无公共点,利用判别式小于零得![]() .由弦长公式可求底边AB长,利用点
.由弦长公式可求底边AB长,利用点![]() 到直线
到直线![]() 距离可得高,代入面积公式可得
距离可得高,代入面积公式可得![]() ,根据对勾函数确定其值域.
,根据对勾函数确定其值域.
试题解析:(Ⅰ)依题意得![]() ,则
,则![]() ,
, ![]() .
.
所以椭圆![]() 与抛物线
与抛物线![]() 的一个交点为
的一个交点为![]() ,
,
于是![]()
![]() ,从而
,从而![]() .
.
又![]() ,解得
,解得![]()
所以椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)依题意,直线![]() 的斜率不为0,设直线
的斜率不为0,设直线![]() :
: ![]() ,
,
由![]() ,消去
,消去![]() 整理得
整理得![]() ,由
,由![]() 得
得![]() .
.
由![]() ,消去
,消去![]() 整理得
整理得![]() ,
,
设![]() ,
, ![]() ,则
,则![]() ,
, ![]() ,
,
所以![]()
![]()
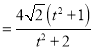 ,
,
![]() 到直线
到直线![]() 距离
距离![]() ,
,
故![]()
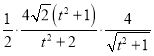
![]() ,
,
令![]() ,则
,则![]()

 ,
,
所以三边形![]() 的面积的取值范围为
的面积的取值范围为 .
.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:
【题目】已知圆M的圆心为M(﹣1,2),直线y=x+4被圆M截得的弦长为 ![]() ,点P在直线l:y=x﹣1上.
,点P在直线l:y=x﹣1上.
(1)求圆M的标准方程;
(2)设点Q在圆M上,且满足 ![]() =4
=4 ![]() ,求点P的坐标;
,求点P的坐标;
(3)设半径为5的圆N与圆M相离,过点P分别作圆M与圆N的切线,切点分别为A,B,若对任意的点P,都有PA=PB成立,求圆心N的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】福利彩票“双色球”中红球的号码可以从01,02,03,…,32,33这33个二位号码中选取,小明利用如图所示的随机数表选取红色球的6个号码,选取方法是从第1行第9列和第10列的数字开始从左到右依次选取两个数字,则第四个被选中的红色球号码为( )
81 47 23 68 63 93 17 90 12 69 86 81 62 93 50 60 91 33 75 85 61 39 85 |
06 32 35 92 46 22 54 10 02 78 49 82 18 86 70 48 05 46 88 15 19 20 49 |
A. 12 B. 33 C. 06 D. 16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】实验杯足球赛采用七人制淘汰赛规则,某场比赛中一班与二班在常规时间内战平,直接进入点球决胜环节,在点球决胜环节中,双方首先轮流罚点球三轮,罚中更多点球的球队获胜;若双方在三轮罚球中未分胜负,则需要进行一对一的点球决胜,即双方各派处一名队员罚点球,直至分出胜负;在前三轮罚球中,若某一时刻胜负已分,尚未出场的队员无需出场罚球(例如一班在先罚球的情况下,一班前两轮均命中,二班前两轮未能命中,则一班、二班的第三位同学无需出场).由于一班同学平时踢球热情较高,每位队员罚点球的命中率都能达到0.8,而二班队员的点球命中串只有0.5,比赛时通过抽签决定一班在每一轮都先罚球.
(1)定义事件![]() 为“一班第三位同学没能出场罚球”,求事件
为“一班第三位同学没能出场罚球”,求事件![]() 发生的概率;
发生的概率;
(2)若两队在前三轮点球结束后打平,则进入一对一点球决胜,一对一球决胜由没有在之前点球大战中出场过的队员主罚点球,若在一对一点球决胜的某一轮中,某对队员射入点球且另一队员未能射入,则比赛结束;若两名队员均射入或者均射失点球,则进行下一轮比赛. 若直至双方场上每名队员都已经出场罚球,则比赛亦结束,双方通过抽签决定胜负,本场比赛中若已知双方在点球大战,以随机变量![]() 记录双方进行一对一点球决胜的轮数,求
记录双方进行一对一点球决胜的轮数,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】极坐标系的极点为直角坐标系的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同,已知曲线C的极坐标方程为ρ=2(cosθ+sinθ).
(1)求C的直角坐标方程;
(2)直线l: 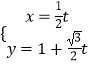 为参数)与曲线C交于A,B两点,与y轴交于E,求|EA|+|EB|的值.
为参数)与曲线C交于A,B两点,与y轴交于E,求|EA|+|EB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x|x﹣a|,a∈R,g(x)=x2﹣1.
(1)当a=1时,解不等式f(x)≥g(x);
(2)记函数f(x)在区间[0,2]上的最大值为F(a),求F(a)的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的首项a1=a,Sn是数列{an}的前n项和,且满足: ![]() =3n2an+
=3n2an+![]() ,an≠0,n≥2,n∈N*.
,an≠0,n≥2,n∈N*.
(1)若数列{an}是等差数列,求a的值;
(2)确定a的取值集合M,使a∈M时,数列{an}是递增数列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com