
【题目】某小组共有A、B、C、D、E五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2)如表所示:
A | B | C | D | E | |
身高 | 1.69 | 1.73 | 1.75 | 1.79 | 1.82 |
体重指标 | 19.2 | 25.1 | 18.5 | 23.3 | 20.9 |
(1)从该小组身高低于1.80的同学中任选2人,求选到的2人身高都在1.78以下的概率
(2)从该小组同学中任选2人,求选到的2人的身高都在1.70以上且体重指标都在[18.5,23.9)中的概率.
【答案】
(1)解:从身高低于1.80的同学中任选2人,其一切可能的结果组成的基本事件有:
(A,B),(A,C),(A,D),(B,C),(B,D),(C,D)共6个.
由于每个同学被选到的机会均等,因此这些基本事件的出现是等可能的.
选到的2人身高都在1.78以下的事件有:(A,B),(A,C),(B,C)共3个.
因此选到的2人身高都在1.78以下的概率为p= ![]() ;
;
(2)解:从该小组同学中任选2人,其一切可能的结果组成的基本事件有:
(A,B),(A,C),(A,D),(A,E),(B,C),(B,D),(B,E),(C,D),(C,E),(D,E)共10个.
由于每个同学被选到的机会均等,因此这些基本事件的出现是等可能的.
选到的2人的身高都在1.70以上且体重指标都在[18.5,23.9)中的事件有:
(C,D)(C,E),(D,E)共3个.
因此选到的2人的身高都在1.70以上且体重指标都在[18.5,23.9)中的概率p= ![]() .
.
【解析】(1)写出从身高低于1.80的同学中任选2人,其一切可能的结果组成的基本事件,查出选到的2人身高都在1.78以下的事件,然后直接利用古典概型概率计算公式求解;.(2)写出从该小组同学中任选2人,其一切可能的结果组成的基本事件,查出选到的2人的身高都在1.70以上且体重指标都在[18.5,23.9)中的事件,利用古典概型概率计算公式求解.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】为了解某社区居民的家庭年收入所年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:
收入x (万元) | 8.2 | 8.6 | 10.0 | 11.3 | 11.9 |
支出y (万元) | 6.2 | 7.5 | 8.0 | 8.5 | 9.8 |
据上表得回归直线方程 ![]() =
= ![]() x+
x+ ![]() ,其中
,其中 ![]() =0.76,
=0.76, ![]() =
= ![]() ﹣
﹣ ![]()
![]() ,据此估计,该社区一户收入为15万元家庭年支出为( )
,据此估计,该社区一户收入为15万元家庭年支出为( )
A.11.4万元
B.11.8万元
C.12.0万元
D.12.2万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某个品牌的U盘进行寿命追踪调查,所得情况如下面频率分布直方图所示. 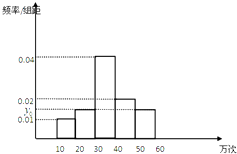
(1)图中纵坐标y0处刻度不清,根据图表所提供的数据还原y0;
(2)根据图表的数据按分层抽样,抽取20个U盘,寿命为1030万次之间的应抽取几个;
(3)从(2)中抽出的寿命落在1030万次之间的元件中任取2个元件,求事件“恰好有一个寿命为1020万次,一个寿命为2030万次”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)在R上存在导数f′(x),x∈R,有f(﹣x)+f(x)=x2 , 在(0,+∞)上f′(x)<x,若f(4﹣m)﹣f(m)≥8﹣4m.则实数m的取值范围为( )
A.[﹣2,2]
B.[2,+∞)
C.[0,+∞)
D.(﹣∞,﹣2]∪[2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,满足a1=3,a4=12,数列{bn}满足b1=4,b4=20,且{bn﹣an}为等比数列.
(1)求数列{an}和{bn}的通项公式;
(2)求数列{bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() .(x>0)
.(x>0)
(1)函数f(x)在区间(0,+∞)上是增函数还是减函数?证明你的结论;
(2)若当x>0时,f(x)> ![]() 恒成立,求正整数k的最大值.
恒成立,求正整数k的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一盒中装有各色球12只,其中5个红球,4个黑球,2个白球,1个绿球;从中随机取出1球.求:
(1)取出的1球是红球或黑球的概率;
(2)取出的1球是红球或黑球或白球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com