
分析 由累加法求出an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)=2n+1+4,由此能求出数列|{an}的前n项和.
解答 解:∵数列|{an}满足a1=8,且${a_{n+1}}-{a_n}={2^{n+1}}$(n∈N*),
∴an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)
=8+22+23+…+2n
=6+$\frac{2(1-{2}^{n})}{1-2}$=2n+1+4,
∴数列|{an}的前n项和:
${S}_{n}={2}^{2}+{2}^{3}+…+{2}^{n+1}+4n$
=$\frac{4(1-{2}^{n})}{1-2}+4n$=2n+2+4n-4.
故答案为:2n+2+4n-4.
点评 本题考查数列的前n项和的求法,是中档题,解题时要认真审题,注意累加法的合理运用.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
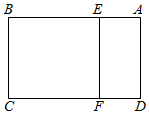 如图,在矩形ABCD中,AD=$\sqrt{5}$,AB=3,E、F分别为AB边、CD边上一点,且AE=DF=l,现将矩形ABCD沿EF折起,使得平面ADFE⊥平面BCFE,连接AB、CD,则所得三棱柱ABE-DCF的侧面积比原矩形ABCD的面积大约多(取$\sqrt{5}$≈2.236)( )
如图,在矩形ABCD中,AD=$\sqrt{5}$,AB=3,E、F分别为AB边、CD边上一点,且AE=DF=l,现将矩形ABCD沿EF折起,使得平面ADFE⊥平面BCFE,连接AB、CD,则所得三棱柱ABE-DCF的侧面积比原矩形ABCD的面积大约多(取$\sqrt{5}$≈2.236)( )| A. | 68% | B. | 70% | C. | 72% | D. | 75% |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{π}{3}$ | B. | $-\frac{π}{6}$ | C. | $-\frac{5π}{6}$ | D. | $-\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $2\sqrt{2}$ | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com