
【题目】(A)在直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的参数方程为
的参数方程为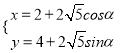 (
(![]() 为参数),
为参数), ![]() 是曲线
是曲线![]() 上的动点,
上的动点, ![]() 为线段
为线段![]() 的中点,设点
的中点,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求![]() 的坐标方程;
的坐标方程;
(2)若射线![]() 与曲线
与曲线![]() 异于极点的交点为
异于极点的交点为![]() ,与曲线
,与曲线![]() 异于极点的交点为
异于极点的交点为![]() ,求
,求![]() .
.
 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的方程是
的方程是![]() ,圆
,圆![]() 的参数方程是
的参数方程是![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)分别求直线![]() 和圆
和圆![]() 的极坐标方程;
的极坐标方程;
(2)射线![]() (其中
(其中![]() )与圆
)与圆![]() 交于
交于![]() 两点,与直线
两点,与直线![]() 交于点
交于点![]() ,射线
,射线![]() 与圆
与圆![]() 交于
交于![]() 两点,与直线
两点,与直线![]() 交于点
交于点![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四个命题:
①在回归分析中, ![]() 可以用来刻画回归效果,
可以用来刻画回归效果, ![]() 的值越大,模型的拟合效果越好;
的值越大,模型的拟合效果越好;
②在独立性检验中,随机变量![]() 的值越大,说明两个分类变量有关系的可能性越大;
的值越大,说明两个分类变量有关系的可能性越大;
③在回归方程![]() 中,当解释变量
中,当解释变量![]() 每增加1个单位时,预报变量
每增加1个单位时,预报变量![]() 平均增加1个单位;
平均增加1个单位;
④两个随机变量相关性越弱,则相关系数的绝对值越接近于1;
其中真命题是:
A. ①④ B. ②④ C. ①② D. ②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某智能手机制作完成之后还需要依次通过三道严格的审核程序,第一道审核、第二道审核、第三道审核通过的概率分别为![]() ,
,![]() ,
,![]() ,每道程序是相互独立的,且一旦审核不通过就停止审核,每部手机只有三道程序都通过才能出厂销售.
,每道程序是相互独立的,且一旦审核不通过就停止审核,每部手机只有三道程序都通过才能出厂销售.
(1)求审核过程中只通过两道程序的概率;
(2)现有3部该智能手机进入审核,记这3部手机可以出厂销售的部数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在心理学研究中,常采用对比试验的方法评价不同心理暗示对人的影响,具体方法如下:将参加试验的志愿者随机分成两组,一组接受甲种心理暗示,另一组接受乙种心理暗示,通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用,现有6名男志愿者![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 和4名
和4名![]() ,
, ![]() ,
, ![]() ,
, ![]() ,从中随机抽取5人接受甲种心理暗示,另5人接受乙种心理暗示.
,从中随机抽取5人接受甲种心理暗示,另5人接受乙种心理暗示.
(Ⅰ)求接受甲种心理暗示的志愿者中包含![]() 但不包含
但不包含![]() 的频率.
的频率.
(Ⅱ)用![]() 表示接受乙种心理暗示的女志愿者人数,求
表示接受乙种心理暗示的女志愿者人数,求![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子内装有8张卡片,每张卡片上面写着1个数字,这8个数字各不相同,且奇数有3个,偶数有5个.每张卡片被取出的概率相等.
(Ⅰ)如果从盒子中一次随机取出2张卡片,并且将取出的2张卡片上的数字相加得到一个新数,求所得新数是偶数的概率;
(Ⅱ)现从盒子中一次随机取出1张卡片,每次取出的卡片都不放回盒子,若取出的卡片上写着的数是偶数则停止取出卡片,否则继续取出卡片.设取出了![]() 次才停止取出卡片,求
次才停止取出卡片,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com