练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】函数f（x）=log （x2﹣4x﹣5）的单调递减区间为 ．

    【答案】（5，+∞）
    【解析】解：要使函数有意义，则x2﹣4x﹣5＞0，即x＞5或x＜﹣1．
    设t=x2﹣4x﹣5，则当x＞5时，函数t=x2﹣4x﹣5单调递增，
    当x＜﹣1时，函数t=x2﹣4x﹣5单调递减．
    ∵函数y=log t，在定义域上为单调递减函数，
    ∴根据复合函数的单调性之间的关系可知，
    当x＞5时，函数f（x）单调递减，
    即函数f（x）的递减区间为（5，+∞）．
    所以答案是：（5，+∞）
    【考点精析】本题主要考查了复合函数单调性的判断方法的相关知识点，需要掌握复合函数f[g(x)]的单调性与构成它的函数u=g(x)，y=f(u)的单调性密切相关，其规律：“同增异减”才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知O为坐标原点，向量 =（sinα，1）， =（cosα，0）， =（﹣sinα，2），点P是直线AB上的一点，且 = ．
    （1）若O，P，C三点共线，求tanα的值；
    （2）在（Ⅰ）条件下，求 +sin2α的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在一次国际学术会议上，来自四个国家的五位代表被安排坐在一张圆桌，为了使他们能够自由交谈，事先了解到的情况如下：

    甲是中国人，还会说英语．

    乙是法国人，还会说日语．

    丙是英国人，还会说法语．

    丁是日本人，还会说汉语．

    戊是法国人，还会说德语．

    则这五位代表的座位顺序应为（ ）

    A. 甲丙丁戊乙 B. 甲丁丙乙戊

    C. 甲乙丙丁戊 D. 甲丙戊乙丁

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知幂函数f（x）=（m2﹣m﹣1）x﹣5m﹣3在（0，+∞）上是增函数，又g（x）=loga （a＞1）．
    （1）求函数g（x）的解析式；
    （2）当x∈（t，a）时，g（x）的值域为（1，+∞），试求a与t的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知曲线C的参数方程为 ( 为参数)，以直角坐标系原点为极点，Ox轴正半轴为极轴建立极坐标系．
    （1）求曲线C的极坐标方程;
    （2）若直线l的极坐标方程为 ，求直线l被曲线C截得的弦长.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在正方体ABCD﹣A1B1C1D1中，棱长为a，E是棱DD1的中点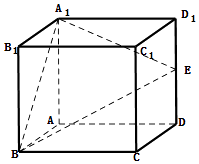

    （1）求三棱锥E﹣A1B1B的体积；
    （2）在棱C1D1上是否存在一点F，使B1F∥平面A1BE？证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】李庄村电费收取有以下两种方案供农户选择：
    方案一：每户每月收管理费2元，月用电不超过30度每度0.5元，超过30度时，超过部分按每度0.6元．
    方案二：不收管理费，每度0.58元．
    （1）求方案一收费L（x）元与用电量x（度）间的函数关系；
    （2）李刚家九月份按方案一交费35元，问李刚家该月用电多少度？
    （3）李刚家月用电量在什么范围时，选择方案一比选择方案二更好？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，AB是⊙O的直径，P是⊙O所在平面外一点，PA垂直于⊙O所在平面，且PA=AB=10，设点C为⊙O上异于A、B的任意一点．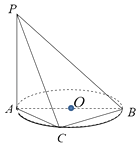

    （1）求证：BC⊥平面PAC；
    （2）若AC=6，求三棱锥C﹣PAB的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f（x）=丨x+a+1丨+丨x-丨，（a＞0）。

    (1)证明：f（x）≥5；

    （2）若f（1）＜6成立，求实数a的取值范围。

    查看答案和解析>>

    同步练习册答案