
【题目】设函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的最大值;
的最大值;
(2)令![]() ,
,![]() 其图象上任意一点
其图象上任意一点![]() 处切线的斜率
处切线的斜率![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)当![]() ,
,![]() ,方程
,方程![]() 有唯一实数解,求正数
有唯一实数解,求正数![]() 的值.
的值.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)利用导数求函数的单调区间即得函数的最大值.(2)由题得![]() ,
,![]() .再求右边二次函数的最大值即得
.再求右边二次函数的最大值即得![]() .(3)转化为
.(3)转化为![]() 有唯一实数解,设
有唯一实数解,设![]() ,再研究函数在定义域内有唯一的零点得解.
,再研究函数在定义域内有唯一的零点得解.
(1)依题意,知![]() 的定义域为
的定义域为![]() ,
,
当![]() 时,
时,![]() ,
,
![]() ,
,
令![]() ,解得
,解得![]() .(∵
.(∵![]() )
)
因为 ![]() 有唯一解,所以
有唯一解,所以![]() ,当
,当![]() 时,
时,![]() ,此时
,此时![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,此时
,此时![]() 单调递减,
单调递减,
所以![]() 的极大值为
的极大值为![]() ,此即为最大值.
,此即为最大值.
(2)![]() ,
,![]() ,则有
,则有![]() ,在
,在![]() 上恒成立,
上恒成立,
所以![]() ,
,![]() .
.
当![]() 时,
时,![]() 取得最大值
取得最大值![]() ,所以
,所以![]() .
.
(3)因为方程![]() 有唯一实数解,
有唯一实数解,
所以![]() 有唯一实数解,
有唯一实数解,
设![]() ,
,
则![]() ,令
,令![]() ,
,![]() ,
,
因为![]() ,
,![]() ,所以
,所以![]() (舍去),
(舍去),![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,
,![]() 取最小值
取最小值![]() .
.
则![]() ,即
,即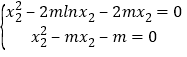 ,
,
所以![]() ,因为
,因为![]() ,所以
,所以![]() (*)
(*)
设函数![]() ,因为当
,因为当![]() 时,
时,
![]() 是增函数,所以
是增函数,所以![]() 至多有一解,
至多有一解,
因为![]() ,所以方程(*)的解为
,所以方程(*)的解为![]() ,即
,即![]() ,解得
,解得![]() .
.


科目:高中数学 来源: 题型:
【题目】甲题型:给出如图数阵表格形式,表格内是按某种规律排列成的有限个正整数.

(1)记第一行的自左至右构成数列![]() ,
,![]() 是
是![]() 的前
的前![]() 项和,试求;
项和,试求;
(2)记![]() 为第
为第![]() 列第
列第![]() 行交点的数字,观察数阵请写出
行交点的数字,观察数阵请写出![]() 表达式,若
表达式,若![]() ,试求出
,试求出![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在以下命题中:
①三个非零向量![]() ,
,![]() ,
,![]() 不能构成空间的一个基底,则
不能构成空间的一个基底,则![]() ,
,![]() ,
,![]() 共面;
共面;
②若两个非零向量![]() ,
,![]() 与任何一个向量都不能构成空间的一个基底,则
与任何一个向量都不能构成空间的一个基底,则![]() ,
,![]() 共线;
共线;
③对空间任意一点![]() 和不共线的三点
和不共线的三点![]() ,
,![]() ,
,![]() ,若
,若![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() 四点共面
四点共面
④若![]() ,
,![]() 是两个不共线的向量,且
是两个不共线的向量,且![]() ,则
,则![]() 构成空间的一个基底
构成空间的一个基底
⑤若![]() 为空间的一个基底,则
为空间的一个基底,则![]() 构成空间的另一个基底;
构成空间的另一个基底;
其中真命题的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学举行了一次“数学基础知识竞赛”活动.为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为![]() )进行统计.按照
)进行统计.按照![]() 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在![]() 的数据).
的数据).


(1)求样本容量![]() 和频率分布直方图中的
和频率分布直方图中的![]() ,
,![]() 的值;
的值;
(2)在选取的样本中,从竞赛成绩在80分以上(含80分)的学生中随机抽取2名学生参加“市级数学基础知识竞赛”,求所抽取的2名学生中恰有一人得分在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若某产品的直径长与标准值的差的绝对值不超过![]() 时,则视为合格品,否则视为不合格品.在近期一次产品抽样检查中,从某厂生产的此种产品中,随机抽取5000件进行检测,结果发现有50件不合格品.计算这50件不合格品的直径长与标准值的差(单位:
时,则视为合格品,否则视为不合格品.在近期一次产品抽样检查中,从某厂生产的此种产品中,随机抽取5000件进行检测,结果发现有50件不合格品.计算这50件不合格品的直径长与标准值的差(单位:![]() )将所得数据分组,得到如下频率分布表:
)将所得数据分组,得到如下频率分布表:

(1)将上面表格中缺少的数据填充完整;
(2)估计该厂生产的此种产品中,不合格的直径长与标准值的差落在区间![]() 内的概率
内的概率
(3)现对该厂这种产品的某个批次进行检查,结果发现有20件不合格品,据此估算这批产品中的合格品的件数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|1<x<3},集合B={x|2m<x<1-m}.
(1)当m=-1时,求A∪B;
(2)若AB,求实数m的取值范围;
(3)若A∩B=,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
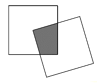
【题目】现有一个关于平面图形的命题:如图所示,同一平面内有两个边长都是a的正方形,其中一个正方形的某顶点在另一个正方形的中心,则这两个正方形重叠部分的面积恒为![]() ,类比到空间,有两个棱长均为a的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为__________.
,类比到空间,有两个棱长均为a的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为__________.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com