
【题目】2016年某招聘会上,有5个条件很类似的求职者,把他们记为A,B,C,D,E,他们应聘秘书工作,但只有2个秘书职位,因此5人中仅有2人被录用,如果5个人被录用的机会相等,分别计算下列事件的概率:
(1)C得到一个职位
(2)B或E得到一个职位.
【答案】
(1)解:5人中有2人被录用的基本事件共有10个,分别为:
(A,B),(A,C),(A,D),(A,E),(B,C),(B,D),(B,E),(C,D),(C,E),(D,E),
C得到一职位包含的基本事件有4个,分别为(A,C),(B,C),(C,D),(C,E),
∴C得到一个职位的概率P1= ![]()
(2)解:B或E得到一个职位,包含的基本事件个数有7个,分别为:
(A,B),(A,E),(B,C),(B,D),(B,E),(C,E),(D,E),
∴B或E得到一个职位的概率P2= ![]()
【解析】(1)利用列举法求出5人中有2人被录用的基本事件共有10个,C得到一职位包含的基本事件有4个,由此能求出C得到一个职位的概率.(2)利用列举法求出B或E得到一个职位,包含的基本事件个数,由此能求出B或E得到一个职位的概率.


 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:高中数学 来源: 题型:
【题目】如今我们的互联网生活日益丰富,除了可以很方便地网购,网上叫外卖也开始成为不少人日常生活中不可或缺的一部分.为了解网络外卖在![]() 市的普及情况,
市的普及情况, ![]() 市某调查机构借助网络进行了关于网络外卖的问卷调查,并从参与调查的网民中抽取了200人进行抽样分析,得到表格:(单位:人)
市某调查机构借助网络进行了关于网络外卖的问卷调查,并从参与调查的网民中抽取了200人进行抽样分析,得到表格:(单位:人)
经常使用网络外卖 | 偶尔或不用网络外卖 | 合计 | |
男性 | 50 | 50 | 100 |
女性 | 60 | 40 | 100 |
合计 | 110 | 90 | 200 |
(1)根据表中数据,能否在犯错误的概率不超过![]() 的前提下认为
的前提下认为![]() 市使用网络外卖的情况与性别有关?
市使用网络外卖的情况与性别有关?
(2)①现从所抽取的女网民中利用分层抽样的方法再抽取5人,再从这5人中随机选出3人赠送外卖优惠券,求选出的3人中至少有2人经常使用网络外卖的概率;
②将频率视为概率,从![]() 市所有参与调查的网民中随机抽取10人赠送礼品,记其中经常使用网络外卖的人数为
市所有参与调查的网民中随机抽取10人赠送礼品,记其中经常使用网络外卖的人数为![]() ,求
,求![]() 的数学期望和方差.
的数学期望和方差.
参考公式:  ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,PA=PC=5,PB=4,AB=BC=2 ![]() ,∠ACB=30°,PA=PC=5,PB=4,AB=BC=2
,∠ACB=30°,PA=PC=5,PB=4,AB=BC=2 ![]() ,∠ACB=30°.
,∠ACB=30°. 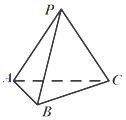
(1)求证:AC⊥PB;
(2)求三棱锥P﹣ABC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ln(1+|x|)﹣ ![]() ,则使得f(x)>f(2x﹣1)成立的取值范围是( )
,则使得f(x)>f(2x﹣1)成立的取值范围是( )
A.(﹣∞, ![]() )∪(1,+∞)?
)∪(1,+∞)?
B.( ![]() ,1)
,1)
C.(- ![]() ,
, ![]() )?
)?
D.(﹣∞,﹣ ![]() ,)
,) ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知极坐标系的极点在平面直角坐标系的原点![]() 处,极轴与
处,极轴与![]() 轴的正半轴重合,且长度单位相同;曲线
轴的正半轴重合,且长度单位相同;曲线![]() 的方程是
的方程是![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),设
),设![]() , 直线
, 直线![]() 与曲线
与曲线![]() 交于
交于 ![]() 两点.
两点.
(1)当![]() 时,求
时,求![]() 的长度;
的长度;
(2)求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C:9x2+4y2=36,直线l:  (t为参数)
(t为参数)
(Ⅰ)写出曲线C的参数方程,直线l的普通方程;
(Ⅱ)过曲线C上任意一点P作与l夹角为30°的直线,交l于点A,求|PA|的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,已知曲线
中,已知曲线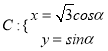 (
(![]() 为参数),在以原点
为参数),在以原点![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立的机坐标系中,直线
轴的非负半轴为极轴建立的机坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)过点![]() 且与直线
且与直线![]() 平行的直线
平行的直线![]() 交
交![]() 于
于![]() 两点,求点
两点,求点![]() 到
到![]() 两点的距离之积.
两点的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面向量 ![]() ,
, ![]() 满足|
满足| ![]() |=1,|
|=1,| ![]() |=2.
|=2.
(1)若 ![]() 与
与 ![]() 的夹角θ=120°,求|
的夹角θ=120°,求| ![]() +
+ ![]() |的值;
|的值;
(2)若(k ![]() +
+ ![]() )⊥(k
)⊥(k ![]() ﹣
﹣ ![]() ),求实数k的值.
),求实数k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应国家治理环境污染的号召,增强学生的环保意识,宿州市某中学举行了一次环保知识竞赛,共有900名学生参加了这次竞赛,为了解本次竞赛的成绩情况,从中抽取了l00学生的成绩进行统计,成绩频率分布直方图如图所示.估计这次测试中成绩的众数为;平均数为;中位数为 . (各组平均数取中值计算,保留整数) 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com