
(2006
广东,10)对任意的两个实数对(a,b)和(c,d),规定:(a,b)=(c,d),当且仅当a=c,b=d;运算“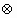 ”为:(a,b)
”为:(a,b)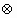 (c,d)=(ac-bd,bc+ad);运算“
(c,d)=(ac-bd,bc+ad);运算“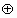 ”为:(a,b)
”为:(a,b)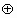 (c,d)=(a+c,b+d).设p、q
(c,d)=(a+c,b+d).设p、q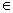 R,若(1,2)
R,若(1,2)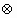 (p,q)=(5,0),则(1,2)
(p,q)=(5,0),则(1,2)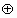 (p,q)等于
(p,q)等于
[
]|
A .(0,-4) |
B .(0,2) |
|
C .(4,0) |
D .(2,0) |
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:044
(2006
广东,19)已知公比为q(0<q<1)的无穷等比数列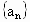 各项的和为9,无穷等比数列
各项的和为9,无穷等比数列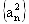 各项的和为
各项的和为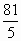 .
.
(1)
求数列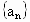 的首项
的首项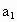 和公比q;
和公比q;
(2)
对给定的k(k=1,2,…,n),设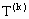 是首项为
是首项为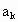 ,公差为
,公差为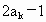 的等差数列.求数列
的等差数列.求数列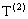 的前10项之和;
的前10项之和;
(3)
设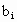 为数列
为数列 的第i项,
的第i项,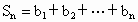 ,求
,求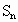 ,并求正整数m(m>1),使得
,并求正整数m(m>1),使得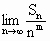 存在且不等于零.
存在且不等于零.
(
注:无穷等比数列各项的和即当 时该无穷等比数列前n项和的极限)
时该无穷等比数列前n项和的极限)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com