【题目】若样本
的平均数是
，方差是
，则对样本
，下列结论正确的是 ( )
A. 平均数为14，方差为5 B. 平均数为13，方差为25
C. 平均数为13，方差为5 D. 平均数为14，方差为2
【答案】C
【解析】
根据平均数和方差的定义和性质进行求解即可．
∵样本1+x1，1+x2，1+x3，…，1+xn的平均数是12，方差为5，
∴1+x1+1+x2+1+x3+…+1+xn=12n，
即x1+x2+x3+…+xn=12n﹣n=11n，
方差S2=
[（1+x1﹣12）2+（1+x2﹣12）2+…+（1+xn﹣12）2]=[（x1﹣11）2+（x2﹣11）2+…+（xn﹣11）2]=5，
则（2+x1+2+x2+…+2+xn）=
=13，
样本2+x1，2+x2，…，2+xn的方差S2=[（2+x1﹣13）2+（2+x2﹣13）2+…+（2+xn﹣13）2]
=[（x1﹣11）2+（x2﹣11）2+…+（xn﹣11）2]=5，
故选：C．
科目：高中数学 来源： 题型：
【题目】若命题p：函数y=x2﹣2x的单调递增区间是[1，+∞），命题q：函数y=x﹣ 
的单调递增区间是[1，+∞），则（ ）
A.p∧q是真命题
B.p∨q是假命题
C.非p是真命题
D.非q是真命题
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知不等式
的解集为(1，t)，记函数
.
(1)求证：函数y＝f(x)必有两个不同的零点；
(2)若函数y＝f(x)的两个零点分别为
，
，试将
表示成以
为自变量的函数，并求的取值范围；
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知向量 
=（cosx+sinx，2sinx）， 
=（cosx﹣sinx，cosx）．令f（x）= ．
（1）求f（x）的最小正周期；
（2）求f（x）在[ 
， 
]上的单调递增区间．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设关于x的一元二次方程
，其中a，b是某范围内的随机数，分别在下列条件下，求上述方程有实根的概率．
(1)若随机数a，b∈{1,2,3,4,5,6}；
(2)若a是从区间[0,5]中任取的一个数，b是从区间[2,4]中任取的一个数．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下图是我国2008年至2014年生活垃圾无害化处理量（单位：亿吨）的折线图.
（Ⅰ）由折线图看出，可用线性回归模型拟合y与t的关系，请用相关系数加以说明；
（Ⅱ）建立y关于t的回归方程（系数精确到0.01），预测2016年我国生活垃圾无害化处理量.
附注：
参考数据：
，
，
，
≈2.646.
参考公式：相关系数
回归方程
中斜率和截距的最小二乘估计公式分别为：
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】阅读如图所示的程序框图，则该算法的功能是（ ）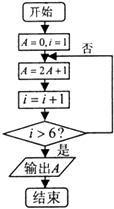 
A.计算数列{2n﹣1}前5项的和
B.计算数列{2n﹣1}前5项的和
C.计算数列{2n﹣1}前6项的和
D.计算数列{2n﹣1}前6项的和
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知f（x）=ax3﹣3x2+1（a＞0），定义h（x）=max{f（x），g（x）}= 
．
（1）求函数f（x）的极值；
（2）若g（x）=xf'（x），且存在x∈[1，2]使h（x）=f（x），求实数a的取值范围；
（3）若g（x）=lnx，试讨论函数h（x）（x＞0）的零点个数．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
