
分析 (Ⅰ)根据直线平行和平行线的距离求出满足条件的直线方程即可;
(Ⅱ)法一:根据方程组求出P的坐标,结合直线垂直的关系求出满足条件的直线方程即可;
法二:根据直线平行,设直线l的方程为x-2y+4+λ(x+y-2)=0,根据直线的垂直关系求出直线的斜率,求出参数的值,从而求出直线方程即可.
解答 解:(Ⅰ) 设与直线x-2y+1=0平行的直线方程为x-2y+c=0,--------(1分)
在直线x-2y+1=0上任取一点P(1,1),
依题意P到直线x-2y+c=0的距离为$\frac{{|{1-2+c}|}}{{\sqrt{1+4}}}=2\sqrt{5}$,解得:c=11或c=-9-------------------------------(4分)
所求直线方程为:x-2y+11=0或x-2y-9=0-----------------------(5分)
(Ⅱ)法一:由方程组$\left\{\begin{array}{l}x-2y+4=0\\ x+y-2=0\end{array}$,得$\left\{\begin{array}{l}x=0\\ y=2\end{array}$,------------------(7分)
即P(0,2).l3:2x+3y+1=0的斜率为${k_3}=-\frac{2}{3}$
∵l⊥l3,∴$k=\frac{3}{2}$,--------------------------(10分)(l3斜率(1分),k3k=-(11分),结论1分)
∴直线l的方程为$y-2=\frac{3}{2}x$,
即l:3x-2y+4=0.----------------------------------------------------------(12分)(不整理不扣分)
法二:∵直线l过直线l1和l2的交点,
∴可设直线l的方程为x-2y+4+λ(x+y-2)=0,
即(1+λ)x+(λ-2)y+4-2λ=0.l3:2x+3y+1=0的斜率为${k_3}=-\frac{2}{3}$
∵l⊥l3,∴$k=\frac{3}{2}$,
∴3(λ-2)+2(λ+1)=0,
∴λ=$\frac{4}{5}$,
∴直线l的方程为3x-2y+4=0,(对照解法一相应给分)
点评 本题考查了求直线方程问题,考查直线的平行和垂直关系,考查平行线间的距离,是一道中档题.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 20 | C. | 26 | D. | 40 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
y 人数 x | 价格满意度 | |||||
| 1 | 2 | 3 | 4 | 5 | ||
| 服 务 满 意 度 | 1 | 1 | 1 | 2 | 2 | 0 |
| 2 | 2 | 1 | 3 | 4 | 1 | |
| 3 | 3 | 7 | 8 | 8 | 4 | |
| 4 | 1 | 4 | 6 | 4 | 1 | |
| 5 | 0 | 1 | 2 | 3 | 1 | |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{-1+5i}{5}$ | B. | $\frac{-1+7i}{5}$ | C. | 1+i | D. | $\frac{-1+5i}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{a(2a+l)}{{2\sqrt{{a^2}+{b^2}}}}$ | B. | $\frac{a+l}{{2\sqrt{{a^2}+{b^2}}}}$ | C. | $\frac{a(l-2a)}{{2\sqrt{{a^2}+{b^2}}}}$ | D. | $\frac{al}{{2\sqrt{{a^2}+{b^2}}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 28个 | B. | 21个 | C. | 35个 | D. | 56个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
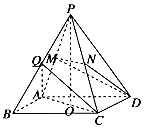 如图,正四棱锥P-ABCD各棱长都为2,点O,M,N,Q分别是AC,PA,PC,PB的中点.
如图,正四棱锥P-ABCD各棱长都为2,点O,M,N,Q分别是AC,PA,PC,PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{π}{4}$,0) | B. | ($\frac{π}{8}$,0) | C. | ($\frac{π}{2}$,0) | D. | ($\frac{5π}{24}$,0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com