
(本小题满分12分)
已知四棱锥的底面是矩形,侧棱长相等,棱锥的高为4,其俯视图如图所示.
(1)作出此四棱锥的主视图和侧视图,并在图中标出相关的数据;
(2)求该四棱锥的侧面积 .
.
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:解答题
(本题满分14分)
如图所示,在正三棱柱ABC -A1B1C1中,底面边长和侧棱长都是2,D是侧棱CC1上任意一点,E是A1B1的中点。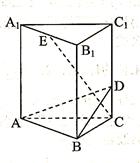
(I)求证:A1B1//平面ABD;
(II)求证:AB⊥CE;
(III)求三棱锥C-ABE的体积。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
如图所示,平面PAD⊥平面ABCD,ABCD为正方形,PA⊥AD,且PA=AD=2,E,F,G分别是线段PA,PD,CD的中点。
(1)求证:BC//平面EFG;
(2)求三棱锥E—AFG的体积。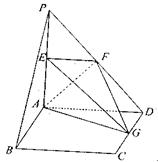
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
如图,四边形ABCD为正方形,四边形BDEF为矩形,AB=2BF,E丄平面ABCD,G为EF中点.
(1)求证:CF//平面
(2) 求证:平面ASG丄平面CDG;
(3)求二面角C—FG—B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题13分)
一个用鲜花做成的花柱,它的下面是一个直径为2m、高为4m的圆柱形物体,上面是一个直 径为2m的半球形体,如果每平方米大约需要鲜花200朵,那么装饰这个花柱大约需要多少朵鲜花(
径为2m的半球形体,如果每平方米大约需要鲜花200朵,那么装饰这个花柱大约需要多少朵鲜花( 取3.1)?
取3.1)?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
一个四棱锥的三视图如图所示:
(1)根据图中标出的尺寸画出直观图(不要求写画法步骤);
(2)求三棱锥A-PDC的体积;高考资源网
(3)试在PB上求点M,使得CM∥平面PDA并加以证明。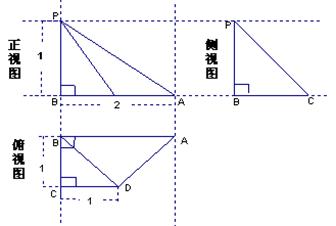
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com