
【题目】已知函数![]() 是偶函数,且
是偶函数,且![]() ,
,![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的值域;
的值域;
(2)设![]() R,求函数
R,求函数![]() 的最小值
的最小值![]() ;
;
(3)对(2)中的![]() ,若不等式
,若不等式![]() 对于任意的
对于任意的![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)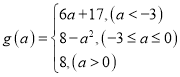 (3)
(3)![]()
【解析】
(1)由函数![]() 是偶函数,可得
是偶函数,可得![]() ,即可求出
,即可求出![]() ,进而可求出
,进而可求出![]() 与
与![]() 的表达式,再由
的表达式,再由![]() 时,函数
时,函数![]() 和
和![]() 都是单调递增函数,可知函数
都是单调递增函数,可知函数![]() 在
在![]() 上单调递增,从而可求出
上单调递增,从而可求出![]() 的值域;
的值域;
(2)![]() ,令
,令![]() ,由(1)知
,由(1)知![]() ,则
,则![]() ,然后利用二次函数的单调性可求得
,然后利用二次函数的单调性可求得![]() 的最小值
的最小值![]() ;
;
(3)当![]() 时,
时,![]() ,则
,则![]() ,整理得
,整理得![]() ,由于
,由于![]() ,则
,则![]() 对于任意的
对于任意的![]() 恒成立,只需令
恒成立,只需令![]() 大于
大于![]() 在
在![]() 上的最大值,求解即可.
上的最大值,求解即可.
(1)因为函数![]() 是偶函数,所以
是偶函数,所以![]() ,解得
,解得![]() .
.
故![]() ,
,![]() .
.
当![]() 时,函数
时,函数![]() 和
和![]() 都是单调递增函数,
都是单调递增函数,
故函数![]() 在
在![]() 上单调递增,
上单调递增,
![]() ,
,![]() ,
,
所以当![]() 时,函数
时,函数![]() 的值域是
的值域是![]() .
.
(2)![]() ,
,
令![]() ,由(1)知
,由(1)知![]() ,则
,则![]() ,
,
因为二次函数![]() 开口向上,对称轴为
开口向上,对称轴为![]() ,
,
故![]() 时,
时,![]() 在
在![]() 上单调递增,最小值为
上单调递增,最小值为![]() ;
;
![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,最小值为
上单调递增,最小值为![]() ;
;
![]() 时,
时,![]() 在
在![]() 上单调递减,最小值为8.
上单调递减,最小值为8.
故函数![]() 的最小值
的最小值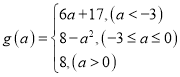 .
.
(3)当![]() 时,
时,![]() ,
,
则![]() 即
即![]() ,整理得
,整理得![]() ,
,
因为![]() ,所以
,所以![]() 对于任意的
对于任意的![]() 恒成立,
恒成立,
令![]() ,
,
只需令![]() 大于
大于![]() 在
在![]() 上的最大值即可.
上的最大值即可.
在![]() 上任取
上任取![]() ,且
,且![]() ,则
,则![]() ,
,![]() ,
,
则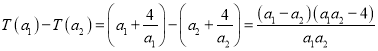 ,
,
当![]() 时,
时,![]() ,则
,则![]() ,即
,即![]() ,故
,故![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,则
,则![]() ,即
,即![]() ,故
,故![]() 在
在![]() 上单调递减;
上单调递减;
所以函数![]() 在
在![]() 上的最大值为
上的最大值为![]() ,
,
故![]() .
.
所以实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】(2017·全国卷Ⅲ文,18)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高气温 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高气温位于各区间的频率估计最高气温位于该区间的概率.
(1)估计六月份这种酸奶一天的需求量不超过300瓶的概率;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元).当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C![]() ,直线
,直线![]() (
(![]() 为参数)
为参数)
(1)写出曲线C的参数方程和直线l的普通方程;
(2)过曲线C上任意一点P作与l夹角为30°的直线,交l于点A,求|PA|的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国南宋时期的著名数学家秦九韶在他的著作《数学九章》中提出了秦九韶算法来计算多项式的值,在执行如图算法的程序框图时,若输入的n=5,x=2,则输出V的值为( ) 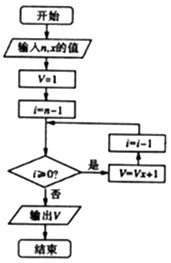
A.15
B.31
C.63
D.127
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=x3﹣3x+2+m(m>0),在区间[0,2]上存在三个不同的实数a,b,c,使得以f(a),f(b),f(c)为边长的三角形是直角三角形,则m的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有甲乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表.
优秀 | 非优秀 | 总计 | |
甲班 | 10 | ||
乙班 | 30 | ||
总计 | 105 |
已知在全部105人中随机抽取1人为优秀的概率为![]() .
.
(1)请完成上面的列联表;
(2)根据列联表的数据,若按95%的可靠性要求,能否认为“成绩与班级有关系”?
参考公式:K2=![]()
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】f(x)是定义在R上的奇函数,对x,y∈R都有f(x+y)=f(x)+f(y),且当x>0时,f(x)<0,f(-1)=2.
(1)求证:f(x)为奇函数;
(2)求证:f(x)是R上的减函数;
(3)求f(x)在[-2,4]上的最值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com