【题目】已知曲线C的极坐标方程是
，以极点为原点，极轴为x轴的正半轴建立平面直角坐标系，曲线C经过伸缩变换
得到曲线E，直线l：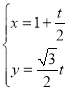
（t为参数）与曲线E交于A，B两点，
（1）设曲线C上任一点为
，求
的最小值；
（2）求出曲线E的直角坐标方程，并求出直线l被曲线E截得的弦AB长；
口算能手系列答案科目：高中数学 来源： 题型：
【题目】数列
,定义
为数列的一阶差分数列,其中
.
(1)若
,试断是否是等差数列,并说明理由；
(2)若
证明
是等差数列,并求数列的通项公式；
(3)对(2)中的数列,是否存在等差数列
,使得
对一切
都成立,若存在,求出数列的通项公式；若不存在,请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系xOy中，直线l的参数方程为
（t为参数），以O为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ（ρ﹣2sinθ）＝1．
（1）求C的直角坐标方程；
（2）设直线l与y轴相交于P，与曲线C相交于A、B两点，且|PA|+|PB|＝2，求点O到直线l的距离．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图是国家统计局今年4月11日发布的2018年3月到2019年3月全国居民消费价格的涨跌幅情况折线图．（注：2019年2月与2018年2月相比较称同比，2019年2月与2019年1月相比较称环比），根据该折线图，下列结论错误的是（ ）
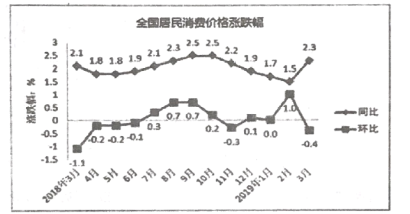
A.2018年3月至2019年3月全国居民消费价格同比均上涨
B.2018年3月至2019年3月全国居民消费价格环比有涨有跌
C.2019年3月全国居民消费价格同比涨幅最大
D.2019年3月全国居民消费价格环比变化最快
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系xOy中，直线l的参数方程为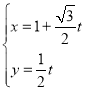
（t为参数），在以O为极点，x轴正半轴为极轴的极坐标系中，曲线C的极坐标方程为ρsin2θ＝4cosθ．
（1）求直线l的普通方程与曲线C的直角坐标方程；
（2）若直线l与x轴的交点为F，直线l与曲线C的交点为A、B，求|FA|+|FB|的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，将边长为1的正方形ABCD沿x轴正向滚动，先以A为中心顺时针旋转，当B落在x轴时，又以B为中心顺时针旋转，如此下去，设顶点C滚动时的曲线方程为
，则下列说法不正确的是
A.
恒成立B.
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下表列出了10名5至8岁儿童的体重x(单位kg)(这是容易测得的)和体积y(单位dm3)(这是难以测得的)，绘制散点图发现，可用线性回归模型拟合y与x的关系：
体重x | 17.00 10.50 13.80 15.70 11.90 10.20 15.00 17.80 16.00 12.10 |
体积y | 16. 70 10.40 13.50 15.70 11.60 10.00 14.50 17.50 15.40 11.70 |
(1)求y关于x的线性回归方程
(系数精确到0.01)；
(2)某5岁儿童的体重为13.00kg，估测此儿童的体积．
附注：参考数据：
，
，
，
，
，
，137×14=1918.00．
参考公式：回归方程中斜率和截距的最小二乘法估计公式分别为：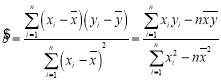
，
．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
