
【题目】已知一个动圆与已知圆Q1:(x+2)2+y2=![]() 外切,与圆Q2:(x-2)2+y2=
外切,与圆Q2:(x-2)2+y2=![]() 内切,(1) 试求这个动圆圆心的轨迹方程;(2)设直线
内切,(1) 试求这个动圆圆心的轨迹方程;(2)设直线![]() 与(1)中动圆圆心轨迹交于A、B两点,坐标原点O到直线
与(1)中动圆圆心轨迹交于A、B两点,坐标原点O到直线![]() 的距离为
的距离为![]() ,求△AOB面积的最大值。
,求△AOB面积的最大值。
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)由两圆位置关系得动圆圆心与Q1,Q2距离之和为定值,再根据椭圆定义确定轨迹为椭圆,最后根据定义中数值对应几何意义求a,b(2)先设直线方程y=kx+m,再根据O到直线![]() 的距离为
的距离为![]() 得m2=
得m2=![]() (k2+1),由三角形面积公式知△AOB面积取最大值对应弦长AB取最大值,因此联立直线方程与椭圆方程,消y得关于x的一元二次方程,结合韦达定理,利用弦长公式求AB的长,最后根据基本不等式求弦长最值
(k2+1),由三角形面积公式知△AOB面积取最大值对应弦长AB取最大值,因此联立直线方程与椭圆方程,消y得关于x的一元二次方程,结合韦达定理,利用弦长公式求AB的长,最后根据基本不等式求弦长最值
试题解析:解:(1)设椭圆的半焦距为c,依题意有
所以c=![]() ,b=1.所以所求椭圆方程为
,b=1.所以所求椭圆方程为![]() +y2=1.
+y2=1.
(2)设A(x1,y1),B(x2,y2).
①当AB⊥x轴时,|AB|=![]() .
.
②当AB与x轴不垂直时,设直线AB的方程为y=kx+m.
由已知![]() =
=![]() ,得m2=
,得m2=![]() (k2+1).
(k2+1).
把y=kx+m代入椭圆方程,
整理得(3k2+1)x2+6kmx+3m2-3=0,
所以x1+x2=![]() ,x1x2=
,x1x2=![]() .
.
所以|AB|2=(1+k2)(x2-x1)2=
(1+k2)![]() =
=
![]() =
=![]() =
=
3+![]() =3+
=3+![]() (k≠0)≤3+
(k≠0)≤3+![]() =4.
=4.
当且仅当9k2=![]() ,即k=±
,即k=±![]() 时等号成立.
时等号成立.
此时Δ=12(3k2+1-m2)>0,
当k=0或不存在时,|AB|=![]() ,综上所述,|AB|max=2.
,综上所述,|AB|max=2.
所以当|AB|最大时,△AOB面积取得最大值
S=![]() ×|AB|max×
×|AB|max×![]() =
=![]() .
.


 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案科目:高中数学 来源: 题型:
【题目】某连锁经营公司所属5个零售店某月的销售额和利润额资料如下表:

(1)若销售额和利润额具有相关关系,用最小二乘法计算利润额y对销售额x的回归直线方程;
(2)据(1)的结果估计当销售额为1亿元时的利润额.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(文科)在下列结论中①“![]() ”为真是“
”为真是“![]() ”为真的充分不必要条件;②“
”为真的充分不必要条件;②“ ![]() ”为假是“
”为假是“![]() ”为真的充分不必要条件;③“
”为真的充分不必要条件;③“ ![]() ”为真是“
”为真是“![]() ”为假的充分不必要条件;④“
”为假的充分不必要条件;④“ ![]() ” 为真是“
” 为真是“![]() ”为假充分不必要条件.正确的是__________.
”为假充分不必要条件.正确的是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一河南旅游团到安徽旅游.看到安徽有很多特色食品,其中水果类较有名气的有:怀远石榴、砀山梨、徽州青枣等19种,点心类较有名气的有:一品玉带糕、徽墨酥、八公山大救驾等38种,小吃类较有名气的有:符离集烧鸡、无为熏鸭、合肥龙虾等57种.该旅游团的游客决定按分层抽样的方法从这些特产中买6种带给亲朋品尝.
(Ⅰ)求应从水果类、点心类、小吃类中分别买回的种数;
(Ⅱ)若某游客从买回的6种特产中随机抽取2种送给自己的父母,
①列出所有可能的抽取结果;
②求抽取的2种特产均为小吃的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
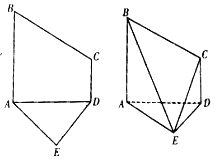
【题目】已知五边形![]() 是由直角梯形
是由直角梯形![]() 和等腰直角三角形
和等腰直角三角形![]() 构成,如图所示,
构成,如图所示, ![]() ,
, ![]() ,
, ![]() ,且
,且![]() ,将五边形
,将五边形![]() 沿着
沿着![]() 折起,且使平面
折起,且使平面![]() 平面
平面![]() .
.
(Ⅰ)若![]() 为
为![]() 中点,边
中点,边![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(Ⅱ)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班50位同学周考数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50)、[50,60)、[60,70)、[70,80)、[80,90)、[90,100]. 
(1)求图中[80,90)的矩形高的值,并估计这50人周考数学的平均成绩;
(2)根据直方图求出这50人成绩的众数和中位数(精确到0.1);
(3)从成绩在[40,60)的学生中随机选取2人,求这2人成绩分别在[40,50)、[50,60)的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司2016年前三个月的利润(单位:百万元)如下:
月份 | 1 | 2 | 3 |
利润 | 2 | 3.9 | 5.5 |
(1)求利润![]() 关于月份
关于月份![]() 的线性回归方程;
的线性回归方程;
(2)试用(1)中求得的回归方程预测4月和5月的利润;
(3)试用(1)中求得的回归方程预测该公司2016年从几月份开始利润超过1000万?
相关公式: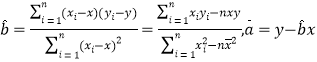 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)若数列{an}是的递增等差数列,其中的a3=5,且a1,a2,a5成等比数列,
(1)求{an}的通项公式;
(2)设bn= ![]() ,求数列{bn}的前项的和Tn.
,求数列{bn}的前项的和Tn.
(3)是否存在自然数m,使得![]() <Tn<
<Tn<![]() 对一切n∈N*恒成立?若存在,求出m的值;
对一切n∈N*恒成立?若存在,求出m的值;
若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com