
 ��n��N*����SnΪ����{bn}��ǰn��ͣ���ʹSn��2010��������С������n��ֵ��
��n��N*����SnΪ����{bn}��ǰn��ͣ���ʹSn��2010��������С������n��ֵ��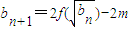 ��n��N*��������f��x���Ľ���ʽ�����bn+1��bn�Ĺ�ϵʽ���Ӷ�ȷ������������{bn}����1Ϊ���࣬2Ϊ���ȵĵȱ����У����ݵȱ����е�ǰn���ʽ��ʾ��Sn�����벻��ʽ�м������������n����Сֵ��
��n��N*��������f��x���Ľ���ʽ�����bn+1��bn�Ĺ�ϵʽ���Ӷ�ȷ������������{bn}����1Ϊ���࣬2Ϊ���ȵĵȱ����У����ݵȱ����е�ǰn���ʽ��ʾ��Sn�����벻��ʽ�м������������n����Сֵ��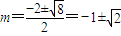 ����8�֣�
����8�֣�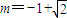 ʱ������d=a3-a2=m2+m-m=m2=
ʱ������d=a3-a2=m2+m-m=m2=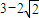 ����9�֣�
����9�֣�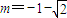 ʱ������
ʱ������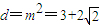 ����10�֣�
����10�֣�


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��֪����f��x��=Asin����x+�գ���x��R��A��0���أ�0��|��|��
��֪����f��x��=Asin����x+�գ���x��R��A��0���أ�0��|��|��| �� |
| 2 |
A��f(x)=2sin(��x+
| ||
B��f(x)=2sin(2��x+
| ||
C��f(x)=2sin(��x+
| ||
D��f(x)=2sin(2��x+
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 |
| 3 |
| f��(x) |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| x |
| a |
| b |
| x |
| 4c2 |
| k(k+c) |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���Ϻ�ģ�� ���ͣ������
| x |
| a |
| b |
| x |
| 4c2 |
| k(k+c) |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������һģ ���ͣ������
| 1 |
| 3 |
| f��(x) |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com