
| 7 |
| cosA |
| cosC |
| ||
2b-
|
| π |
| 6 |
 解:(1)∵
解:(1)∵| cosA |
| cosC |
| ||
2b-
|
| cosA |
| cosC |
| ||
2sinB-
|
| 3 |
| 3 |
| 3 |
| ||
| 2 |
| π |
| 6 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 28 | ||
2+
|
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 3 |


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源:中学教材全解 高中数学必修4 B版(配人民教育出版社实验教科书) 人教版 B版 题型:044
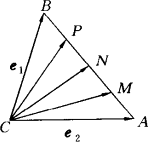
如图,已知△ABC中,M、N、P顺次是AB的四等分点,![]() ,试用e1、e2表示
,试用e1、e2表示![]() .
.
查看答案和解析>>
科目:高中数学 来源:2012年人教A版高中数学必修四2.3平面向量基本定理及坐标表示(一)(解析版) 题型:解答题
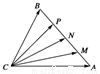
如图,已知△ABC中,M、N、P顺次是AB的四等分点,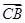 =e1,
=e1,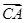 =e2,试用e1,e2表示
=e2,试用e1,e2表示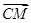 、
、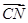 、
、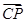 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com