练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，小明从街道的E处出发，先到F处与小红会合，再一起到位于G处的老年公寓参加志愿者活动，则小明到老年公寓可以选择的最短路径条数为（　　）

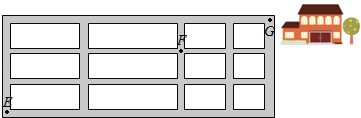
    A. 9B. 12C. 18D. 24

    【答案】C

    【解析】

    从E点到F点最短的走法，无论怎样走，一定包括4段，其中2段方向相同，另2段方向相同，每种最短走法，即是从4段中选出2段走东向的，选出2段走北向的，利用组合的知识，即可求解。

    从E到F，每条东西向的街道被分成2段，每条南北向的街道被分称2段，

    从E点到F点最短的走法，无论怎样走，一定包括4段，其中2段方向相同，另2段方向相同，每种最短走法，即是从4段中选出2段走东向的，选出2段走北向的，

    故共有种走法，

    同理从F到G，最短的走法，有种走法，

    所以小明到老年公寓可以选择的最短路径条数为种走法，故选C。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】下列说法中，错误的是（ ）

    A. 若命题，，则命题，

    B. “”是“”的必要不充分条件

    C. “若，则、中至少有一个不小于”的逆否命题是真命题

    D. ，

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率,顶点到直线的距离为，椭圆内接四边形（点在椭圆上）的对角线相交于点，且.

    (1)求椭圆的标准方程；

    (2)求的面积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设的内角所对的边为,则下列命题正确的是_____．

    ①若，则； ②若，则；

    ③若，则； ④若，则．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对于函数f（x），若存在x0∈R，使f（x0）=x0，则称x0是f（x）的一个不动点，已知f（x）=x2+ax+4在[1，3]恒有两个不同的不动点，则实数a的取值范围______.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数

    （1）若函数在定义域内单调递增，求的取值范围；

    （2）若且关于的方程在上恰有两个不相等的实数根，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直角梯形ABCD中，BC⊥DC，AE⊥DC，M，N分别是AD，BE的中点，将三角形ADE沿AE折起，则下列说法正确的是________(填序号)．

    ①不论D折至何位置(不在平面ABC内)，都有MN∥平面DEC；②不论D折至何位置，都有MN⊥AE；③不论D折至何位置(不在平面ABC内)，都有MN∥AB；④在折起过程中，一定存在某个位置，使EC⊥AD.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，已知曲线的参数方程为，（为参数），直线的参数方程为（为参数，为实数），直线与曲线交于 两点.

    （1）若，求的长度；

    （2）当面积取得最大值时（为原点），求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若展开式中前三项系数成等差数列，求：

    （1）展开式中含x的一次幂的项；

    （2）展开式中所有x 的有理项；

    （3）展开式中系数最大的项。

    查看答案和解析>>

    同步练习册答案