Question

已知数列｛b_n｝是等差数列，b₁=1,b₁+b₂+…+b₁₀=100.

 

(Ⅰ)求数列｛b_n｝的通项b_n;

(Ⅱ)设数列｛a_n｝的通项a_n=lg(1+),记S_n是数列｛a_n｝的前n项和，试比较S_n与lgb_n+1的大小，并证明你的结论.

Answer 1

(Ⅰ)设数列｛b_n｝的公差为d，由题意得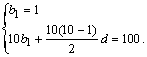

 

解得    ∴b_n=2n-1.?

 

(Ⅱ)由b_n=2n-1,知?

S_n=lg(1+1)+lg(1+)+……+lg(1+)

=lg［(1+1)(1+)……(1+)］,?

 

lgb_n+1=lg.?

因此要比较S_n与lgb_n+1的大小，可先比较(1+1)(1+)……(1+ )与的大小.?

取n=1有(1+1)＞,?取n=2有(1+1)(1+)＞……

由此推测(1+1)(1+)……(1+)＞.①若①式成立，则由对数函数性质

可断定：S_n＞lgb_n+1.?

 

下面用数学归纳法证明①式.?

(i)当n=1时已验证①式成立.?

(ii)假设当n=k(k≥1)时，①式成立，即(1+1) (1+)……(1+)＞ .?

那么，当n=k+1时，(1+1) (1+)……(1+)＞(1+)

=(2k+2)，?

 

 ∵[(2k+2)]²-[]²==>0

 

∴(2k+2)＞=.

因而(1+1)(1+)……(1+)(1+)＞.?

这就是说①式当n=k+1时也成立.?

由(i)，(ii)知①式对任何正整数n都成立.?

由此证得：S_n＞lgb_n+1.