
【题目】设函数![]() .
.
(1)若方程![]() 在
在![]() 上有根,求实数
上有根,求实数![]() 的取值范围;
的取值范围;
(2)设![]() ,若对任意的
,若对任意的![]() ,
,![]() 都有
都有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由题意可得函数h(x)=f(x)﹣3x=x2+|x﹣1|﹣3x+2a 在![]() 上有零点,
上有零点,
h(0)h(1)=(2a+1)(2a﹣2)<0,由此求得a的范围;
(2)对任意的![]() ,
,![]() 都有
都有![]() ,即
,即![]() ,分别求两边函数的最值即可.
,分别求两边函数的最值即可.
(1)∵方程f(x)=3x在![]() 上有根,
上有根,
∴函数h(x)=f(x)﹣3x=x2+|x﹣1|﹣3x+2a 在![]() 上有零点.
上有零点.
由于在![]() 上,h(x)=f(x)﹣3x=x2﹣4x+2a+1是减函数,
上,h(x)=f(x)﹣3x=x2﹣4x+2a+1是减函数,
故有h(0)h(1)=(2a+1)(2a﹣2)<0,
求得![]() a<1.
a<1.
(2)对任意的![]() ,
,![]() 都有
都有![]() ,
,
即![]()
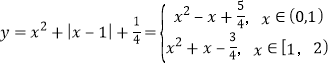 ,
,
![]() 时,
时,![]() 的最小值为
的最小值为![]() ,
,
![]() 时,
时,![]() 的最小值为
的最小值为![]()
故![]() 在
在![]() 上的最小值为
上的最小值为![]()
![]() (x)=cos2x+2asinx
(x)=cos2x+2asinx![]() =﹣sin2x+2asinx+1
=﹣sin2x+2asinx+1![]()
令t=sinx,因为![]() ,所以﹣1≤t≤1且y=﹣t2+2at+1
,所以﹣1≤t≤1且y=﹣t2+2at+1![]() ,其对称轴为t=a,
,其对称轴为t=a,
故a≤﹣1时,y=﹣t2+2at+1![]() 在[﹣1,1]上是减函数,最大值为﹣4a,
在[﹣1,1]上是减函数,最大值为﹣4a,
此时﹣4a<1,a>![]() ,无解;
,无解;
当﹣1<a<1时,当t=a时y有最大值a2![]() +1,
+1,
此时a2![]() +1<1,即
+1<1,即![]() ,又﹣1<a<1,∴0<a<1
,又﹣1<a<1,∴0<a<1
当a≥1时,y=﹣t2+2at+1![]() 在[﹣1,1]上是增函数,最大值为0
在[﹣1,1]上是增函数,最大值为0
此时0<1,显然恒成立,
综上:a的范围![]()


科目:高中数学 来源: 题型:
【题目】某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据:
x | 6 | 8 | 10 | 12 |
y | 2 | 3 | 5 | 6 |
(1)请在图中画出上表数据的散点图;

![]() 请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;
![]() 试根据
试根据![]() 求出的线性回归方程,预测记忆力为9的同学的判断力.
求出的线性回归方程,预测记忆力为9的同学的判断力.
相关公式: .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知,如图,在直二面角![]() 中,四边形
中,四边形![]() 是边长为
是边长为![]() 的正方形,
的正方形,![]() ,且
,且![]() .
.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)在线段![]() (不包含端点)上是否存在点
(不包含端点)上是否存在点![]() ,使得
,使得![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ;若存在,写出
;若存在,写出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机掷两枚质地均匀的骰子,它们向上的点数之和不超过5的概率记为p1,点数之和大于5的概率记为p2,点数之和为偶数的概率记为p3,则
( )
A. p1<p2<p3 B. p2<p1<p3 C. p1<p3<p2 D. p3<p1<p2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,已知三点O(0,0),A(2, ![]() ),B(2
),B(2 ![]() ,
, ![]() ).
).
(1)求经过O,A,B的圆C1的极坐标方程;
(2)以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,圆C2的参数方程为 ![]() (θ是参数),若圆C1与圆C2外切,求实数a的值.
(θ是参数),若圆C1与圆C2外切,求实数a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com