
����Ŀ���ף�����̨����ͬʱ����һ�������������������ָ�껮�֣�ָ����ڻ����100Ϊ��Ʒ�����ڵ���90��С��100Ϊ�ϸ�Ʒ��С��90Ϊ��Ʒ���������ȡ����̨���������������100�����м�⣬�����ͳ�����£�
����ָ�� | [85��90�� | [90��95�� | [95��100�� | [100��105�� | [105��110�� |
������ | 8 | 12 | 40 | 32 | 8 |
������ | 7 | 18 | 40 | 29 | 6 |
��1���Էֱ���Ƽ������һ������������Ϊ��Ʒ�ĸ��ʣ�
��2����������һ�������������Ʒ��ӯ��160Ԫ���ϸ�Ʒ��ӯ��100Ԫ����Ʒ�����20Ԫ���������ij������50�����������Ƽ��������������λ��Ԫ����
��3���Ӽס��һ������������ָ����[90��95���ڵ�����У����÷ֲ�����ķ�����ȡ5��������5������ѡ2��������������������2�������һ��������ĸ��ʣ�
���𰸡���1��![]() ��2��5720��3��
��2��5720��3��![]()
����𡿽⣺��1����Ϊ����Ϊ��Ʒ��Ƶ��Ϊ![]() ��
��
�һ���Ϊ��Ʒ��Ƶ��ԼΪ![]() ��
��
���Թ��Ƽס���������Ϊ��Ʒ�ĸ��ʷֱ�Ϊ![]() ��
��
��2�����������Ʒÿ1����ƽ��������Ϊ��
![]() Ԫ
Ԫ
���Թ��Ƽ���ÿ����1��������Ϊ114.4Ԫ
���Լ���ij������50�����������Ϊ50��114.4=5720Ԫ
��3��������֪������Ӧ��ȡ![]() ��
��
�һ���Ӧ��ȡ![]() ��
��
�Ǽ�����2�����ΪA��B���һ�����3�����Ϊa��b��c��
����5����ѡȡ2���ֱ�ΪAB��Aa��Ab��Ac��Ba��Bb��Bc��ab��ac��bc��10��ȡ��
���������Ĺ���3�֣��ֱ�Ϊab��ac��bc��
���ԣ���2�������һ��������ĸ���![]() ��
��
��������
�������:��1������Ƶ��������������Ƶ�ʣ��������Ƹ��ʣ�2���ȸ���Ƶ�ʼ�����Ʒ���ϸ�Ʒ����Ʒ����Ӧ���ʣ������Ӧ������˵ĺ�Ϊ����3���ȸ��ݷֲ����ȷ����2��3������ö�ٷ�ȷ���¼�����������ȷ��2�������һ����Ļ����¼����������ݹŵ�����ʹ�ʽ�����
�������:�⣺��1����Ϊ����Ϊ��Ʒ��Ƶ��Ϊ![]() ��
��
�һ���Ϊ��Ʒ��Ƶ��ԼΪ![]() ��
��
���Թ��Ƽס���������Ϊ��Ʒ�ĸ��ʷֱ�Ϊ![]() ��
��
��2�����������Ʒÿ1����ƽ��������Ϊ��
![]() Ԫ
Ԫ
���Թ��Ƽ���ÿ����1��������Ϊ114.4Ԫ
���Լ���ij������50�����������Ϊ50��114.4=5720Ԫ
��3��������֪������Ӧ��ȡ![]() ��
��
�һ���Ӧ��ȡ![]() ��
��
�Ǽ�����2�����ΪA��B���һ�����3�����Ϊa��b��c��
����5����ѡȡ2���ֱ�ΪAB��Aa��Ab��Ac��Ba��Bb��Bc��ab��ac��bc��10��ȡ��
���������Ĺ���3�֣��ֱ�Ϊab��ac��bc��
���ԣ���2�������һ��������ĸ���![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ����������ֱ���
����������ֱ���![]() ��
��
��1����A��BC�ߵľ���d��
��2����֤AB��������һ��P��ֱ��AC,BC�ľ���֮�͵���d.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������P-ABC�IJ�����ֱ�������Σ�PA=6������P��ƽ��ABC�ڵ���ͶӰΪ��D��D��ƽ��PAB�ڵ���ͶӰΪ��E������PE���ӳ���AB�ڵ�G.

������֤����G��AB���е㣻
��������ͼ��������E��ƽ��PAC�ڵ���ͶӰF��˵�����������ɣ�������������PDEF�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵ�У���ԭ��Ϊ���㣬x���������Ϊ���Ὠ��������ϵ����֪����C��![]() ��a��0��������P����2����4����ֱ��l�IJ�������Ϊ
��a��0��������P����2����4����ֱ��l�IJ�������Ϊ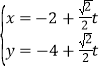 ��tΪ��������l��C�ֱ���M��N.
��tΪ��������l��C�ֱ���M��N.
��1��д��C��ƽ��ֱ������ϵ���̺�l����ͨ���̣�
��2����|PM|��|MN|��|PN|�ɵȱ����У���a��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��R������f��x����log2��![]() a����
a����
����a��1���ⲻ��ʽf��x����1��
������a��0����������t�ʣ���1��0]������f��x��������[t��t+1]�ϵ����ֵ����Сֵ�ĺͲ�����log26����a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() ��,��֪��б��Ϊ
��,��֪��б��Ϊ![]() ��ֱ��
��ֱ��![]() ������
������![]() .������ԭ��
.������ԭ��![]() Ϊ����,
Ϊ����,![]() ���������Ϊ���Ὠ��������ϵ,����
���������Ϊ���Ὠ��������ϵ,����![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]()
(1)д������![]() ����ͨ����;
����ͨ����;
(2)��ֱ��![]() ������
������![]() ��������ͬ�Ľ���
��������ͬ�Ľ���![]() ,��
,��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��b������ֱ�ߣ��������н��ۣ�
��һ������ƽ��![]() ��ʹֱ��
��ʹֱ��![]() ƽ��
ƽ��![]() ��ֱ��
��ֱ��![]() ƽ��
ƽ��![]() ��
��
��һ������ƽ��![]() ��ʹֱ��
��ʹֱ��![]() ƽ��
ƽ��![]() ��ֱ��
��ֱ��![]() ƽ��
ƽ��![]() ��
��
��һ������������ƽ��![]() ��ʹֱ��b��ƽ��
��ʹֱ��b��ƽ��![]() ����һ�����㣬��ֱ��
����һ�����㣬��ֱ��![]() ƽ��
ƽ��![]() .
.
��������ȷ���۵����Ϊ�� ��
A.�ڢ�B.�٢�C.�٢�D.�٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ⳤΪ2��������![]() �У���
����![]() ����
����![]() ���е㣮
���е㣮
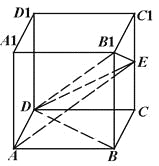
��1����֤��![]() ��
��
��2����֤��![]() ƽ��
ƽ��![]() ��
��
��3��������![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() Ϊ�ȱ������Σ���ƽ��
Ϊ�ȱ������Σ���ƽ��![]() ƽ��
ƽ��![]() ��
��![]() Ϊ
Ϊ![]() �е�.
�е�.

��1����֤��![]() ƽ��
ƽ��![]() ��
��
��2��������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com