
分析 (1)假设存在友好三角形,根据新定义得出结论,
(2)利用正弦定理和新定义得出A1,B1,C1与B的关系,根据内角和得出方程,解出B.
解答 解:(1)①若存在友好三角形,则$\frac{0}{sin{A}_{1}}=\frac{\frac{1}{2}}{sin{A}_{2}}$,显然不成立,故①不存在友好三角形.
②若存在友好三角形,则$\frac{\frac{\sqrt{6}-\sqrt{2}}{4}}{sin{A}_{1}}=\frac{\frac{1}{2}}{sin{A}_{2}}=\frac{\frac{\sqrt{2}}{2}}{sin{A}_{3}}$,∴a1:b1:c1=sinA1:sinA2:sinA3=$\sqrt{6}-\sqrt{2}$:2:2$\sqrt{2}$.∴a1+b1=$\sqrt{6}-\sqrt{2}+2$>2$\sqrt{2}$,
③若存在友好三角形,则$\frac{\frac{\sqrt{6}-\sqrt{2}}{4}}{sin{A}_{1}}=\frac{\frac{\sqrt{6}-\sqrt{2}}{4}}{sin{A}_{2}}=\frac{\frac{\sqrt{3}}{2}}{sin{A}_{3}}$,∴a1:b1:c1=sinA1:sinA2:sinA3=$\sqrt{6}-\sqrt{2}$:$\sqrt{6}-\sqrt{2}$:2$\sqrt{3}$.∴a1+b1=2($\sqrt{6}$-$\sqrt{2}$)<2$\sqrt{3}$.与三角形两根之和大于第三边矛盾.故③不存在友好三角形.
综上,存在友好三角形的是②.
(2)C=180°-70°-B=110°-B.
∴$\frac{cos70°}{sin{A}_{1}}=\frac{cosB}{sin{B}_{1}}=\frac{cos(110°-B)}{sin{C}_{1}}$,即$\frac{sin20°}{sin{A}_{1}}=\frac{sin(90°-B)}{sin{B}_{1}}=\frac{sin(B-20°)}{sin{C}_{1}}$,∴$\frac{sin20°}{{a}_{1}}=\frac{sin(90°-B)}{{b}_{1}}=\frac{sin(B-20°)}{{c}_{1}}$,
∵$\frac{sin{A}_{1}}{{a}_{1}}=\frac{sin{B}_{1}}{{b}_{1}}=\frac{sin{C}_{1}}{{c}_{1}}$,∴sinA1=sin20°,sinB1=sin(90°-B),sinC1=sin(B-20°),
∴A1=20°或160°,B1=90°-B,或B1=90°+B,C1=B-20°或200°-B.
∵A1+B1+C1=180°,∴20°+90°-B+200°-B=180°,或20°+90°+B+B-20°=180°,解得B=65°,或者B=45°.
∴C=45°,或C=65°.
故答案为65°,45°.
点评 本题考查了正弦定理及三角形的相关知识,属于中档题.


 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 只能是x=-1 | |
| B. | 可能是y轴 | |
| C. | 可能在y轴右侧且在直线x=2的左侧 | |
| D. | 可能在y轴左侧且在直线x=-2的右侧 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
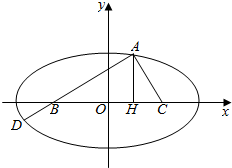 如图,B(-c,0),C(c,0),AH⊥BC,垂足为H,且$\overrightarrow{BH}$=3$\overrightarrow{HC}$.又$\overrightarrow{AD}$=-4$\overrightarrow{DB}$,且A、D同在B、C为焦点的椭圆上,求椭圆的离心率.
如图,B(-c,0),C(c,0),AH⊥BC,垂足为H,且$\overrightarrow{BH}$=3$\overrightarrow{HC}$.又$\overrightarrow{AD}$=-4$\overrightarrow{DB}$,且A、D同在B、C为焦点的椭圆上,求椭圆的离心率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com