
【题目】已知函数![]()
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() ,求a的取值范围.
,求a的取值范围.
【答案】(1)见解析(2)![]()
【解析】
试题分析:(1)先求函数导数![]() ,再按导函数零点讨论:若
,再按导函数零点讨论:若![]() ,无零点,单调;若
,无零点,单调;若![]() ,一个零点
,一个零点![]() ,先减后增;若
,先减后增;若![]() ,一个零点
,一个零点![]() ,先减后增;(2)由单调性确定函数最小值:若
,先减后增;(2)由单调性确定函数最小值:若![]() ,满足;若
,满足;若![]() ,最小值为
,最小值为![]() ,即
,即![]() ;若
;若![]() ,最小值为
,最小值为![]() ,即
,即![]() ,综合可得
,综合可得![]() 的取值范围为
的取值范围为![]() .
.
试题解析:(1)函数![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
①若![]() ,则
,则![]() ,在
,在![]() 单调递增.
单调递增.
②若![]() ,则由
,则由![]() 得
得![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
③若![]() ,则由
,则由![]() 得
得![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
(2)①若![]() ,则
,则![]() ,所以
,所以![]() .
.
②若![]() ,则由(1)得,当
,则由(1)得,当![]() 时,
时,![]() 取得最小值,最小值为
取得最小值,最小值为![]() .从而当且仅当
.从而当且仅当![]() ,即
,即![]() 时,
时,![]() .
.
③若![]() ,则由(1)得,当
,则由(1)得,当![]() 时,
时,![]() 取得最小值,最小值为
取得最小值,最小值为![]() .从而当且仅当
.从而当且仅当![]() ,即
,即![]() 时
时![]() .
.
综上,![]() 的取值范围为
的取值范围为![]() .
.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:高中数学 来源: 题型:
【题目】学校某研究性学习小组在对学生上课注意力集中情况的调查研究中,发现其在40分钟的一节课中,注意力指数![]() 与听课时间
与听课时间![]() (单位:分钟)之间的关系满足如图所示的图象,当
(单位:分钟)之间的关系满足如图所示的图象,当![]() 时,图象是二次函数图象的一部分,其中顶点
时,图象是二次函数图象的一部分,其中顶点![]() ,过点
,过点![]() ;当
;当![]() 时,图象是线段
时,图象是线段![]() ,其中
,其中![]() .根据专家研究,当注意力指数大于62时,学习效果最佳.
.根据专家研究,当注意力指数大于62时,学习效果最佳.

(Ⅰ)试求![]() 的函数关系式;
的函数关系式;
(Ⅱ)教师在什么时段内安排内核心内容,能使得学生学习效果最佳?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2﹣x﹣12≤0},B={x|m+1≤x≤2m﹣1},
(1)当m=3时,求集合A∪B;
(2)若A∪B=A,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)是定义在R上的偶函数,且f(x+2)=f(2-x),当x∈[-2,0]时,f(x)=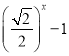 ,则在区间(-2,6)上关于x的方程f(x)-log8(x+2)=0的解的个数为( )
,则在区间(-2,6)上关于x的方程f(x)-log8(x+2)=0的解的个数为( )
A. 4B. 3C. 2D. 1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市公园内的人工湖上有一个以点![]() 为圆心的圆形喷泉,沿湖有一条小径
为圆心的圆形喷泉,沿湖有一条小径![]() ,在
,在![]() 的另一侧建有控制台
的另一侧建有控制台![]() ,
,![]() 和
和![]() 之间均有小径连接(小径均为直路),且
之间均有小径连接(小径均为直路),且![]() ,喷泉中心
,喷泉中心![]() 点距离
点距离![]() 点60米,且
点60米,且![]() 连线恰与
连线恰与![]() 平行,在小径
平行,在小径![]() 上有一拍照点
上有一拍照点![]() ,现测得
,现测得![]() 米,
米, ![]() 米,且
米,且![]() .
.

(I)请计算小径![]() 的长度;
的长度;
(Ⅱ)现打算改建控制台![]() 的位置,其离喷泉尽可能近,在点
的位置,其离喷泉尽可能近,在点![]() 的位置及
的位置及![]() 大小均不变的前提下,请计算
大小均不变的前提下,请计算![]() 距离的最小值;
距离的最小值;
(Ⅲ)一人从小径一端![]() 处向
处向![]() 处匀速前进时,喷泉恰好同时开启,喷泉开启
处匀速前进时,喷泉恰好同时开启,喷泉开启![]() 分钟后的水幕是一个以
分钟后的水幕是一个以![]() 为圆心,半径
为圆心,半径![]() 米的圆形区域(含边界),此人的行进速度是
米的圆形区域(含边界),此人的行进速度是![]() 米/分钟,在这个人行进的过程中他会被水幕沾染,试求实数
米/分钟,在这个人行进的过程中他会被水幕沾染,试求实数![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C过点M(0,-2)、N(3,1),且圆心C在直线x+2y+1=0上.
(1)求圆C的方程;
(2)设直线ax-y+1=0与圆C交于A,B两点,是否存在实数a,使得过点P(2,0)的直线l垂直平分弦AB?若存在,求出实数a的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com