
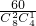 =
=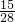
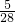 ,P(ξ=1)=
,P(ξ=1)=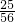 ,P(ξ=3)=
,P(ξ=3)= ,P(ξ=2)=
,P(ξ=2)=
| ξ | 0 | 1 | 2 | 3 |
| p | 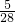 | 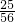 |  |  |



 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
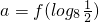 ,b=f(7.5),c=f(-5),则a、b、c的大小关系是
,b=f(7.5),c=f(-5),则a、b、c的大小关系是查看答案和解析>>
科目:高中数学 来源: 题型:解答题
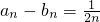 .
.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 ,某植物研究所分两个小组分别独立开展该种子的发芽实验,每次实验种三粒种子,假定某次实验种子至少有一颗发芽则称该次实验成功,如果没有种子发芽,则称该次实验是失败的.
,某植物研究所分两个小组分别独立开展该种子的发芽实验,每次实验种三粒种子,假定某次实验种子至少有一颗发芽则称该次实验成功,如果没有种子发芽,则称该次实验是失败的.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com