
【题目】在△ABC中,角A、B、C对应边分别为a、b、c.
(1)若a=14,b=40,cosB=![]() ,求cosC;
,求cosC;
(2)若a=3,b=![]() ,B=2A,求c的长度.
,B=2A,求c的长度.
科目:高中数学 来源: 题型:
【题目】已知正三棱锥P﹣ABC,点P、A、B、C都在半径为![]() 的球面上,若PA、PB、PC两两互相垂直,则球心到截面ABC的距离为( )
的球面上,若PA、PB、PC两两互相垂直,则球心到截面ABC的距离为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】养正中学新校区内有一块以O为圆心,R(单位:米)为半径的半圆形荒地(如图),校总务处计划对其开发利用,其中弓形BCD区域(阴影部分)用于种植观赏植物,△OBD区域用于种植花卉出售,其余区域用于种植草皮出售。已知种植观赏植物的成本是每平方米20元,种植花卉的利润是每平方米80元,种植草皮的利润是每平方米30元。
(1)设![]() (单位:弧度),用
(单位:弧度),用![]() 表示弓形BCD的面积
表示弓形BCD的面积![]()
(2)如果该校总务处邀请你规划这块土地。如何设计![]() 的大小才能使总利润最大?并求出该最大值
的大小才能使总利润最大?并求出该最大值

查看答案和解析>>
科目:高中数学 来源: 题型:
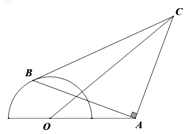
【题目】如图,半圆O的直径为2,A为直径延长线上一点,OA=2,B为半圆上任意一点,以线段AB为腰作等腰直角△ABC(C、O两点在直线AB的两侧),当∠AOB变化时,OC≤m恒成立,则m的最小值为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在 △ABC 中,设 a,b,c 分别是角 A,B,C 的对边,已知向量 ![]() = (a,sinC-sinB),
= (a,sinC-sinB),![]() = (b + c,sinA + sinB),且
= (b + c,sinA + sinB),且![]()
(1) 求角 C 的大小
(2) 若 c = 3, 求 △ABC 的周长的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】点O为坐标原点,直线l经过抛物线C:y2=4x的焦点F.
(Ⅰ)若点O到直线l的距离为![]() , 求直线l的方程;
, 求直线l的方程;
(Ⅱ)设点A是直线l与抛物线C在第一象限的交点.点B是以点F为圆心,|FA|为半径的圆与x轴负半轴的交点.试判断直线AB与抛物线C的位置关系,并给出证明.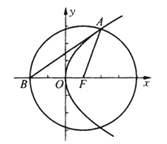
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知实数x,y满足ax<ay(0<a<1),则下列关系式恒成立的是( )
A.![]() >
> ![]()
![]()
B.ln(x2+1)>ln(y2+1)
C.sinx>siny
D.x3>y3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com