
(1)求E的方程;
(2)若直线l过F2,且与轨迹E交于P、Q两点.
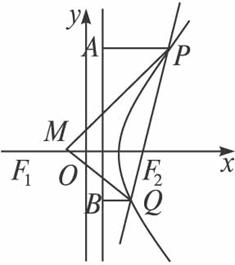
①无论直线l绕点F2如何转动,在x轴上总存在定点M(m,0),使MP⊥QM恒成立,求实数m的值.
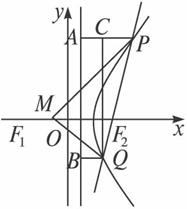
②过P、Q作直线x=![]() 的垂线PA、QB,垂足分别是A、B,记λ=
的垂线PA、QB,垂足分别是A、B,记λ=![]() ,求λ的取值范围.
,求λ的取值范围.
解:(1)由|PF1|-|PF2|=2<|F1F2|知,点P的轨迹E是以F1、F2为焦点的双曲线右支,
由c=2,2a=2,∴b2=3,故轨迹E的方程为x2![]() =1(x≥1).
=1(x≥1).
(2)当直线l的斜率存在时,设直线方程为y=k(x-2),P(x1,y1),Q(x2,y2),与双曲线方程联立消y得(k2-3)x2-4k2x+4k2+3=0,
∴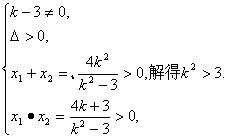
①∵![]() =(x1-m)(x2-m)+y1y2=(x1-m)(x2-m)+k2(x1-2)(x2-2)
=(x1-m)(x2-m)+y1y2=(x1-m)(x2-m)+k2(x1-2)(x2-2)
=(k2+1)x1x2-(2k2+m)(x1+x2)+m2+4k2
=![]() +m2+4k2
+m2+4k2
=![]() +m2.
+m2.
∵MP⊥MQ,∴![]() =0,
=0,
故得3(1-m2)+k2(m2-4m-5)=0对任意的k2>3恒成立,
∴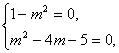 解得m=-1,∴当m=-1时,MP⊥MQ.
解得m=-1,∴当m=-1时,MP⊥MQ.
当直线l的斜率不存在时,由P(2,3)、Q(2,-3)及M(-1,0)知结论成立,
综上,当m=-1时,MP⊥MQ.
②∵a=1,c=2,直线x=![]() 是双曲线的右准线,
是双曲线的右准线,
由双曲线定义得:|PA|=![]() |PF2|=
|PF2|=![]() |PF2|,|QB|=
|PF2|,|QB|=![]() |QF2|,
|QF2|,
方法一:λ=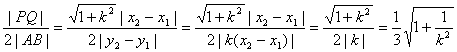 .
.
∵k2>3,∴0<![]() ,故
,故![]() <λ<
<λ<![]() ,
,
注意到直线的斜率不存在时,|PQ|=|AB|,此时λ=![]() ,
,
综上,λ∈[![]() ).
).
方法二:设直线PQ的倾斜角为θ,
由于直线PQ与双曲线右支有两个交点,
∴![]() <θ<
<θ<![]() ,过Q作QC⊥PA,垂足为C,
,过Q作QC⊥PA,垂足为C,
则∠PQC=|![]() -θ|,
-θ|,
∴λ=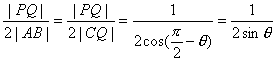 .
.
由![]() <θ<
<θ<![]() ,得
,得![]() <sinθ≤1,故λ∈[
<sinθ≤1,故λ∈[![]() ).
).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| 2 |
| 2 |
| MQ |
| QF |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 2 |
| OA |
| OB |
| OC |
| 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 2 |
| TF1 |
| TF2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 2 |
| TF1 |
| TF2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广西省高三第二次模拟考试文科数学试卷 题型:解答题
已知F1(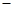 2,0),F2(2,0),点P满足|PF1|-|PF2|=2,记点P的轨迹为S,过点F2作直线
2,0),F2(2,0),点P满足|PF1|-|PF2|=2,记点P的轨迹为S,过点F2作直线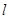 与轨迹S交于P、Q两点,过P、Q作直线x=的垂线PA、QB,垂足分别为A、B,记λ=|AP|·|BQ|.
与轨迹S交于P、Q两点,过P、Q作直线x=的垂线PA、QB,垂足分别为A、B,记λ=|AP|·|BQ|.
(1)求轨迹S的方程;
(2)设点M( 1,0),求证:当λ取最小值时,△PMQ的面积为9.
1,0),求证:当λ取最小值时,△PMQ的面积为9.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com