
【题目】正项等比数列{an},若2a1+3a2=1,a32=9a2a6 .
(1)求数列{an}的通项公式;
(2)设bn=log3a1+log3a2+log3a3+…log3an , 求数列{ ![]() }的前n项和Sn .
}的前n项和Sn .
【答案】
(1)解:依题意,a32=9a2a6=9a3a5,
∴ ![]() =q2=
=q2= ![]() ,
,
解得:q= ![]() 或q=﹣
或q=﹣ ![]() (舍),
(舍),
又∵2a1+3a2=1,即2a1+3 ![]() a1=1,
a1=1,
∴a1= ![]() ,
,
∴数列{an}是首项、公比均为 ![]() 的等比数列,
的等比数列,
∴其通项公式an= ![]()
(2)解:由(1)可知log3an=log3 ![]() =﹣n,
=﹣n,
∴bn=log3a1+log3a2+log3a3+…log3an
=﹣1﹣2﹣…﹣n
=﹣ ![]() ,
,
∴ ![]() =﹣
=﹣ ![]() =﹣2(
=﹣2( ![]() ﹣
﹣ ![]() ),
),
∴数列{ ![]() }的前n项和Sn=﹣2(1﹣
}的前n项和Sn=﹣2(1﹣ ![]() +…+
+…+ ![]() ﹣
﹣ ![]() )
)
=﹣2(1﹣ ![]() )
)
=﹣ ![]() .
.
【解析】(1)通过a32=9a2a6=9a3a5计算可知 ![]() =q2=
=q2= ![]() ,进而可知公比q=
,进而可知公比q= ![]() ,通过2a1+3a2=1可知a1=
,通过2a1+3a2=1可知a1= ![]() ,进而计算可得结论;(2)通过(1)可知log3an=﹣n,从而bn=﹣
,进而计算可得结论;(2)通过(1)可知log3an=﹣n,从而bn=﹣ ![]() ,裂项可知
,裂项可知 ![]() =﹣2(
=﹣2( ![]() ﹣
﹣ ![]() ),并项相加即得结论.
),并项相加即得结论.
【考点精析】解答此题的关键在于理解等比数列的通项公式(及其变式)的相关知识,掌握通项公式:![]() ,以及对数列的前n项和的理解,了解数列{an}的前n项和sn与通项an的关系
,以及对数列的前n项和的理解,了解数列{an}的前n项和sn与通项an的关系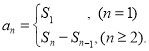 .
.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
【题目】数列![]() 中,
中,![]() 在直线
在直线![]() .
.
(1)求数列{an}的通项公式;
(2)令![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() .
.
(ⅰ)求![]() ;
;
(ⅱ)是否存在整数λ![]() ,使得不等式(-1)nλ<
,使得不等式(-1)nλ<![]() (n∈N
(n∈N![]() )恒成立?若存在,求出λ的取值的集合;若不存在,请说明理由.
)恒成立?若存在,求出λ的取值的集合;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100 个网箱,测量各箱水产品的产量(单位:kg),其频率分布直方图如图:
(Ⅰ)设两种养殖方法的箱产量相互独立,记A表示事件“旧养殖法的箱产量低于50kg,新养殖法的箱产量不低于50kg”,估计A的概率;
(Ⅱ)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
箱产量<50kg | 箱产量≥50kg | |
旧养殖法 | ||
新养殖法 |
(Ⅲ)根据箱产量的频率分布直方图,求新养殖法箱产量的中位数的估计值(精确到0.01).
附:
P(K2≥k) | 0.050 | 0.010 | 0.001 |
K | 3.841 | 6.635 | 10.828 |
K2= ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() sin(ωx﹣
sin(ωx﹣ ![]() )+b(ω>0),且函数图象的对称中心到对称轴的最小距离为
)+b(ω>0),且函数图象的对称中心到对称轴的最小距离为 ![]() ,当x∈[0,
,当x∈[0, ![]() ]时,f(x)的最大值为1.
]时,f(x)的最大值为1.
(1)求函数f(x)的解析式;
(2)将函数f(x)的图象向右平移 ![]() 个单位长度得到函数g(x)图象,若g(x)﹣3≤m≤g(x)+3在x∈[0,
个单位长度得到函数g(x)图象,若g(x)﹣3≤m≤g(x)+3在x∈[0, ![]() ]上恒成立,求实数m的取值范围.
]上恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边是a,b,c,已知2b﹣c=2acosC.
(1)求A;
(2)若4(b+c)=3bc,a=2 ![]() ,求△ABC的面积S.
,求△ABC的面积S.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】分别抛掷两颗骰子各一次,观察向上的点数,求:
(1)两数之和为5的概率;
(2)以第一次向上的点数为横坐标![]() ,第二次向上的点数为纵坐标
,第二次向上的点数为纵坐标![]() 的点
的点![]() 在圆
在圆![]() 内部的概率.
内部的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣1|+|x﹣a|.
(1)若a=2,解不等式f(x)≥2;
(2)若a>1,x∈R,f(x)+|x﹣1|≥1,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知x∈(1,+∞),函数f(x)=ex+2ax(a∈R),函数g(x)=| ![]() ﹣lnx|+lnx,其中e为自然对数的底数.
﹣lnx|+lnx,其中e为自然对数的底数.
(1)若a=﹣ ![]() ,求函数f(x)的单调区间;
,求函数f(x)的单调区间;
(2)证明:当a∈(2,+∞)时,f′(x﹣1)>g(x)+a.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com