
分析 (1)由已知|$\overrightarrow{a}$-$\overrightarrow{b}$|=2,两边平方后即可求得$\overrightarrow{a}$•$\overrightarrow{b}$的值;
(2)由(1)中求得的$\overrightarrow{a}$•$\overrightarrow{b}$的值,进一步求出$|\overrightarrow{a}+\overrightarrow{b}{|}^{2}$得答案;
(3)直接由向量在向量方向上的投影概念求解.
解答 解:(1)由|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=1,|$\overrightarrow{a}$-$\overrightarrow{b}$|=2,
得$|\overrightarrow{a}-\overrightarrow{b}{|}^{2}=|\overrightarrow{a}{|}^{2}-2\overrightarrow{a}•\overrightarrow{b}+|\overrightarrow{b}{|}^{2}=4+1-2\overrightarrow{a}•\overrightarrow{b}=4$,
∴$\overrightarrow{a}•\overrightarrow{b}=\frac{1}{2}$;
(2)∵$|\overrightarrow{a}+\overrightarrow{b}{|}^{2}=|\overrightarrow{a}{|}^{2}+2\overrightarrow{a}•\overrightarrow{b}+|\overrightarrow{b}{|}^{2}=4+2×\frac{1}{2}+1=6$,
∴$|\overrightarrow{a}+\overrightarrow{b}|=\sqrt{6}$;
(3)$\overrightarrow{a}$在$\overrightarrow{b}$上的投影为:$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{b}|}=\frac{1}{2}$.
点评 本题考查平面向量的数量积运算,考查向量模的求法,考查向量在向量方向上投影的求法,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | {x|-2≤x≤1} | B. | {x|1≤x≤3} | C. | {x|0<x≤1} | D. | {x|0<x≤3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 20 | C. | 26 | D. | 40 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 5 | C. | $\sqrt{5}$ | D. | 3$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 2 | C. | 2$\sqrt{5}$ | D. | 2$\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
y 人数 x | 价格满意度 | |||||
| 1 | 2 | 3 | 4 | 5 | ||
| 服 务 满 意 度 | 1 | 1 | 1 | 2 | 2 | 0 |
| 2 | 2 | 1 | 3 | 4 | 1 | |
| 3 | 3 | 7 | 8 | 8 | 4 | |
| 4 | 1 | 4 | 6 | 4 | 1 | |
| 5 | 0 | 1 | 2 | 3 | 1 | |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
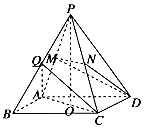 如图,正四棱锥P-ABCD各棱长都为2,点O,M,N,Q分别是AC,PA,PC,PB的中点.
如图,正四棱锥P-ABCD各棱长都为2,点O,M,N,Q分别是AC,PA,PC,PB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com