
【题目】设函数f(x)=|x﹣2|+|x﹣a|,x∈R.
(Ⅰ)求证:当a=﹣1时,不等式lnf(x)>1成立;
(Ⅱ)关于x的不等式f(x)≥a在R上恒成立,求实数a的最大值.
【答案】解:(Ⅰ)证明:当a=﹣1时,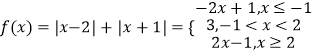 ,
,
故f(x)的最小值为3,
则lnf(x)的最小值为ln3>lne=1,
所以lnf(x)>1成立.
(Ⅱ)由绝对值不等式可得:
f(x)=|x﹣2|+|x﹣a|≥|(x﹣2)﹣(x﹣a)|=|a﹣2|,
再由不等式f(x)≥a在R上恒成立,
可得|a﹣2|≥a,解得a≤1,
故a的最大值为1.
【解析】(Ⅰ)通过讨论x的范围,得到f(x)的分段函数的形式,求出f(x)的最小值,从而证出结论即可;(Ⅱ)求出f(x)的最小值,得到关于a的不等式,解出即可.
【考点精析】利用绝对值不等式的解法对题目进行判断即可得到答案,需要熟知含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx﹣ ![]() x2(a∈R).
x2(a∈R).
(1)若x>0,恒有f(x)≤x成立,求实数a的取值范围;
(2)若a=0,求f(x)在区间[t,t+2](t>0)上的最小值;
(3)若函数g(x)=f(x)﹣x有两个极值点x1 , x2 , 求证: ![]() +
+ ![]() >2ae.
>2ae.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)在R上的导函数为f'(x),对于任意的实数x,都有f'(x)+2017<4034x,若f(t+1)<f(﹣t)+4034t+2017,则实数t的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人的各科成绩如图中的茎叶图所示,则下列说法不正确的是( )
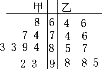
A. 甲、乙两人的各科平均分相同
B. 甲各科成绩的中位数是83,乙各科成绩的中位数是85
C. 甲各科成绩比乙各科成绩稳定
D. 甲各科成绩的众数是89,乙各科成绩的众数为87
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下三个关于圆锥曲线的命题中:
①设A、B为两个定点,K为非零常数,若|PA|-|PB|=K,则动点P的轨迹是双曲线.
②方程![]() 的两根可分别作为椭圆和双曲线的离心率.
的两根可分别作为椭圆和双曲线的离心率.
③双曲线![]() 与椭圆
与椭圆![]() 有相同的焦点.
有相同的焦点.
④已知抛物线![]() ,以过焦点的一条弦AB为直径作圆,则此圆与准线相切.
,以过焦点的一条弦AB为直径作圆,则此圆与准线相切.
其中真命题为_________(写出所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知点![]() 分别是
分别是![]() 的边
的边![]() 的中点,连接
的中点,连接![]() ,现将
,现将![]() 沿
沿![]() 折叠至
折叠至![]() 的位置,连接
的位置,连接![]() .记平面
.记平面![]() 与平面
与平面![]() 的交线为
的交线为![]() ,二面角
,二面角![]() 大小为
大小为![]() .
.
(1)证明: ![]() 平面
平面![]() ;
;
(2)证明:平面![]() 平面
平面![]() ;
;
(3)求平面![]() 与平面
与平面![]() 所成锐二面角大小.
所成锐二面角大小.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2+2x-4y+3=0.
(1)若直线l过点(-2,0)且被圆C截得的弦长为2,求直线l的方程;
(2)从圆C外一点P向圆C引一条切线,切点为M,O为坐标原点,且|PM|=|PO|,求|PM|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某礼品店要制作一批长方体包装盒,材料是边长为![]() 的正方形纸板.如图所示,先在其中相邻两个角处各切去一个边长是
的正方形纸板.如图所示,先在其中相邻两个角处各切去一个边长是![]() 的正方形,然后在余下两个角处各切去一个长、宽分别为
的正方形,然后在余下两个角处各切去一个长、宽分别为![]() 、
、![]() 的矩形,再将剩余部分沿图中的虚线折起,做成一个有盖的长方体包装盒.
的矩形,再将剩余部分沿图中的虚线折起,做成一个有盖的长方体包装盒.

(1)求包装盒的容积![]() 关于
关于![]() 的函数表达式,并求函数的定义域;
的函数表达式,并求函数的定义域;
(2)当![]() 为多少时,包装盒的容积最大?最大容积是多少?
为多少时,包装盒的容积最大?最大容积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某汽车站每天均有3辆开往省城的分为上、中、下等级的客车,某天袁先生准备在该汽车站乘车前往省城办事,但他不知道客车的车况,也不知道发车顺序.为了尽可能乘上上等车,他采取如下策略:先放过一辆,如果第二辆比第一辆好则上第二辆,否则上第三辆.则他乘上上等车的概率为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com