
【题目】已知函数![]() ,函数
,函数![]() ,其中
,其中![]() ,
,![]() 是
是![]() 的一个极值点,且
的一个极值点,且![]() .
.
(1)讨论![]() 的单调性
的单调性
(2)求实数![]() 和a的值
和a的值
(3)证明![]()
【答案】(1)![]() 在区间
在区间![]() 单调递增;(2)
单调递增;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)求出![]() ,在定义域内,再次求导,可得在区间
,在定义域内,再次求导,可得在区间![]() 上
上![]() 恒成立,从而可得结论;(2)由
恒成立,从而可得结论;(2)由![]() ,可得
,可得![]() ,由
,由![]() 可得
可得![]() ,联立解方程组可得结果;(3)由(1)知
,联立解方程组可得结果;(3)由(1)知![]() 在区间
在区间![]() 单调递增,可证明
单调递增,可证明![]() ,取
,取![]() ,可得
,可得![]() ,而
,而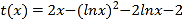 ,利用裂项相消法,结合放缩法可得结果.
,利用裂项相消法,结合放缩法可得结果.
(1)由已知可得函数![]() 的定义域为
的定义域为![]() ,且
,且![]() ,
,
令![]() ,则有
,则有![]() ,由
,由![]() ,可得
,可得![]() ,
,
可知当x变化时,![]() 的变化情况如下表:
的变化情况如下表:
|
| 1 |
|
| - | 0 | + |
|
| 极小值 |
|
![]() ,即
,即![]() ,可得
,可得![]() 在区间
在区间![]() 单调递增;
单调递增;
(2)由已知可得函数![]() 的定义域为
的定义域为![]() ,且
,且![]() ,
,
由已知得![]() ,即
,即![]() ,①
,①
由![]() 可得,
可得,![]() ,②
,②
联立①②,消去a,可得![]() ,③
,③
令![]() ,则
,则![]() ,
,
由(1)知,![]() ,故
,故![]() ,
,![]() 在区间
在区间![]() 单调递增,
单调递增,
注意到![]() ,所以方程③有唯一解
,所以方程③有唯一解![]() ,代入①,可得
,代入①,可得![]() ,
,
![]() ;
;
(3)证明:由(1)知![]() 在区间
在区间![]() 单调递增,
单调递增,
故当![]() 时,
时,![]() ,
,![]() ,
,
可得![]() 在区间
在区间![]() 单调递增,
单调递增,
因此,当![]() 时,
时,![]() ,即
,即![]() ,亦即
,亦即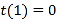 ,
,
这时![]() ,故可得
,故可得![]() ,取
,取![]() ,
,
可得![]() ,而
,而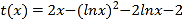 ,
,
故![]()
![]() .
.


科目:高中数学 来源: 题型:
【题目】袋中装有9只球,其中标有数字1,2,3,4的小球各2个,标数字5的小球有1个.从袋中任取3个小球,每个小球被取出的可能性都相等,用![]() 表示取出的3个小球上的最大数字.
表示取出的3个小球上的最大数字.
(1)求取出的3个小球上的数字互不相同的概率;
(2)求随机变量![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程:在平面直角坐标系![]() 中,曲线
中,曲线![]() :
:![]() (
(![]() 为参数),在以平面直角坐标系的原点为极点、
为参数),在以平面直角坐标系的原点为极点、![]() 轴的正半轴为极轴,且与平面直角坐标系
轴的正半轴为极轴,且与平面直角坐标系![]() 取相同单位长度的极坐标系中,曲线
取相同单位长度的极坐标系中,曲线![]() :
:![]() .
.
(1)求曲线![]() 的普通方程以及曲线
的普通方程以及曲线![]() 的平面直角坐标方程;
的平面直角坐标方程;
(2)若曲线![]() 上恰好存在三个不同的点到曲线
上恰好存在三个不同的点到曲线![]() 的距离相等,求这三个点的极坐标.
的距离相等,求这三个点的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x),f′(x)是其导函数且满足f(x)+f′(x)>2,f(1)=2![]() ,则不等式exf(x)>4+2ex的解集为_____
,则不等式exf(x)>4+2ex的解集为_____
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医院拟派2名内科医生、3名外科医生和3名护士共8人组成两个医疗分队,平均分到甲、乙两个村进行义务巡诊,其中每个分队都必须有内科医生、外科医生和护士,则不同的分配方案有
A. 72种 B. 36种 C. 24种 D. 18种
查看答案和解析>>
科目:高中数学 来源: 题型:
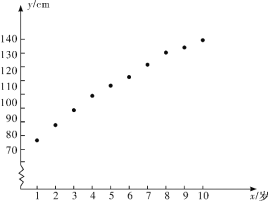
【题目】某地1~10岁男童年龄![]() (单位:岁)与身高的中位数
(单位:岁)与身高的中位数![]() (单位
(单位![]() ,如表所示:
,如表所示:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 76.5 | 88.5 | 96.8 | 104.1 | 111.3 | 117.7 | 124 | 130 | 135.4 | 140.2 |
对上表的数据作初步处理,得到下面的散点图及一些统计量的值.
|
|
|
|
112.45 | 82.50 | 3947.71 | 566.85 |
(1)求![]() 关于
关于![]() 的线性回归方程(回归方程系数精确到0.01);
的线性回归方程(回归方程系数精确到0.01);
(2)某同学认为方程![]() 更适合作为
更适合作为![]() 关于
关于![]() 的回归方程模型,他求得的回归方程是
的回归方程模型,他求得的回归方程是![]() .经调查,该地11岁男童身高的中位数为
.经调查,该地11岁男童身高的中位数为![]() ,与(1)中的线性回归方程比较,哪个回归方程的拟合效果更好?
,与(1)中的线性回归方程比较,哪个回归方程的拟合效果更好?
(3)从6岁~10岁男童中每个年龄阶段各挑选一位男童参加表演(假设该年龄段身高的中位数就是该男童的身高).再从这5位男童中任挑选两人表演“二重唱”,则“二重唱”男童身高满足![]() 的概率是多少?
的概率是多少?
参考公式: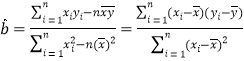 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]() ,下列说法正确的是( )
,下列说法正确的是( )
(1)![]() 是
是![]() 的极大值点 ;(2)函数
的极大值点 ;(2)函数![]() 有且只有1个零点;(3)存在正实数
有且只有1个零点;(3)存在正实数![]() ,使得
,使得![]() 恒成立 ;(4)对任意两个正实数
恒成立 ;(4)对任意两个正实数![]() ,且
,且![]() ,若
,若![]() ,则
,则![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com