
【题目】已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且![]()
(1)求证:不论![]() 为何值,总有平面BEF⊥平面ABC;
为何值,总有平面BEF⊥平面ABC;
(2)当λ为何值时,平面BEF⊥平面ACD ?

科目:高中数学 来源: 题型:
【题目】设在平面上有两个向量a=(cos 2α,sin 2α)(0≤α<π),b=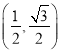 ,a与b不共线.
,a与b不共线.
(1)求证:向量a+b与a-b垂直;
(2)当向量![]() a+b与a-
a+b与a-![]() b的模相等时,求α的大小.
b的模相等时,求α的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】静宁县是甘肃苹果栽培第一大县,中国著名优质苹果基地和重要苹果出口基地.静宁县海拔高、光照充足、昼夜温差大、环境无污染,适合种植苹果.“静宁苹果”以色泽鲜艳、质细汁多,酸甜适度,口感脆甜、货架期长、极耐储藏和长途运输而著名.为检测一批静宁苹果,随机抽取50个,其重量(单位:克)的频数分布表如下:
分组(重量) | [80,85) | [85,90) | [90,95) | [95,100) |
频数(个) | 5 | 10 | 20 | 15 |
(1)根据频数分布表计算苹果的重量在[90,95)的频率;
(2)用分层抽样的方法从重量在[80,85)和[95,100)的苹果中共抽取4个,其中重量在[80,85)的有几个?
(3)在(2)中抽出的4个苹果中,任取2个,求重量在[80,85)和[95,100)中各有1个的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
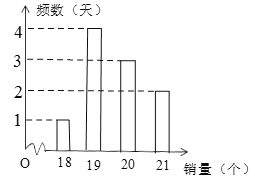
【题目】某商场对某一商品搞活动,已知该商品每一个的进价为3元,销售价为8元,每天售出的第20个及之后的半价出售.该商场统计了近10天的这种商品销量,如图所示:设![]() 为每天商品的销量,
为每天商品的销量,![]() 为该商场每天销售这种商品的的利润.从日利润不少于96元的几天里任选2天,则选出的这2天日利润都是97元的概率为( )
为该商场每天销售这种商品的的利润.从日利润不少于96元的几天里任选2天,则选出的这2天日利润都是97元的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第十三届全运会将在2017年8月在天津举行,组委会在2017年1月对参加接待服务的10名宾馆经理进行为期半月的培训,培训结束,组织了一次培训结业测试,10人考试成绩如下(满分为100分):
75 84 65 90 88 95 78 85 98 82
(Ⅰ)以成绩的十位为茎个位为叶作出本次结业成绩的茎叶图,并计算平均成绩与成绩中位数 ;
(Ⅱ)从本次结业成绩在80分以上的人员中选3人,这3人中成绩在90分(含90分)以上的人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() ,
, ![]() ,设函数
,设函数![]() ,且
,且![]() 的图象过点
的图象过点![]() 和点
和点![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)将![]() 的图象向左平移
的图象向左平移![]() (
(![]() )个单位后得到函数
)个单位后得到函数![]() 的图象.若
的图象.若![]() 的图象上各最高点到点
的图象上各最高点到点![]() 的距离的最小值为1,求
的距离的最小值为1,求![]() 的单调增区间.
的单调增区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com