[题目]已知f=0.f+x+1.的表达式,＞a在x∈[﹣1.1]恒成立.求实数a的取值范围．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】已知f（x）是二次函数，且f（0）=0，f（x+1）=f（x）+x+1，
（1）求f（x）的表达式；
（2）若f（x）＞a在x∈[﹣1，1]恒成立，求实数a的取值范围．

【答案】
（1）解：设f（x）=ax2+bx+c∵f（0）=0∴c=0

∴f（x）=ax2+bxf（x）+x+1=ax2+（b+1）x+1f（x+1）

=a（x+1）2+b（x+1）=ax2+（2a+b）x+a+b∵f（x+1）

=f（x）+x+1∴ax2+（2a+b）x+a+b=ax2+（b+1）x+1

∴ ∴

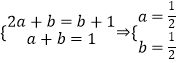（2）解：f（x）＞a在x∈[﹣1，1]恒成立

∴ x＞a在x∈[﹣1，1]恒成立

∴ 在x∈[﹣1，1]恒成立．

∴

【解析】（1）根据函数类型设出函数的解析式，然后根据f（0）=0，f（x+1）=f（x）+x+1，建立两个等式关系，解之即可；（2）要使f（x）＞a在x∈[﹣1，1]恒成立，只需研究函数f（x）在闭区间[﹣1，1]上的最小值即可，利用配方法结合二次函数的性质即可求出f（x）的最小值．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】若，，且|k＋b|＝| －kb|(k＞0)．

（Ⅰ）用k表示数量积；

（Ⅱ）求的最小值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设函数f（x）= x2+ax﹣lnx（a∈R）．
（1）当a=1时，求函数f（x）的极值；
（2）当a＞1时，讨论函数f（x）的单调性；
（3）若对任意a∈（3，4）及任意x1 ， x2∈[1，2]，恒有 m+ln2＞|f（x1）﹣f（x2）|成立，求实数m的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】函数y=Asin（ωx+）（A＞0，ω＞0）在x∈（0，7π）内取到一个最大值和一个最小值，且当x=π时，y有最大值3，当x=6π时，y有最小值﹣3．
（1）求此函数解析式；
（2）写出该函数的单调递增区间；
（3）是否存在实数m，满足不等式Asin（）＞Asin（）？若存在，求出m值（或范围），若不存在，请说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】甲、乙、丙、丁四个物体同时从某一点出发向同一个方向运动，其路程fi（x）（i=1，2，3，4）关于时间x（x≥0）的函数关系式分别为f1（x）=2x﹣1，f2（x）=x3 ， f3（x）=x，f4（x）=log2（x+1），有以下结论：
①当x＞1时，甲走在最前面；
②当x＞1时，乙走在最前面；
③当0＜x＜1时，丁走在最前面，当x＞1时，丁走在最前面；
④丙不可能走在最前面，也不可能走在最后面；
⑤如果它们一直运动下去，最终走在最前面的是甲．
其中，正确结论的序号为（把正确结论的序号都填上，多填或少填均不得分）

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】定义：对于函数f（x），若在定义域内存在实数x，满足f（﹣x）=﹣f（x），则称f（x）为“局部奇函数”．
（1）已知二次函数f（x）=ax2+2x﹣4a（a∈R），试判断f（x）是否为定义域R上的“局部奇函数”？若是，求出满足f（﹣x）=﹣f（x）的x的值；若不是，请说明理由；
（2）若f（x）=2x+m是定义在区间[﹣1，1]上的“局部奇函数”，求实数m的取值范围．
（3）若f（x）=4x﹣m2x+1+m2﹣3为定义域R上的“局部奇函数”，求实数m的取值范围．