
 ,1)的圆M与x轴及直线y=
,1)的圆M与x轴及直线y= x分别相切于A,B两点,另一圆N与圆M外切、且与x轴及直线y=
x分别相切于A,B两点,另一圆N与圆M外切、且与x轴及直线y= x分别相切于C、D两点.
x分别相切于C、D两点.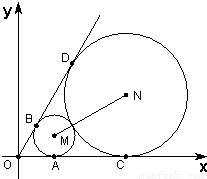
 x分别相切于A,B两点,故半径易知,另一圆N与圆M外切、且与x轴及直线y=
x分别相切于A,B两点,故半径易知,另一圆N与圆M外切、且与x轴及直线y=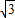 x分别相切于C、D两点,由相似性易得其圆心坐标与半径,依定义写出两圆的方程即可.
x分别相切于C、D两点,由相似性易得其圆心坐标与半径,依定义写出两圆的方程即可.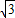 ,1),∴M到x轴的距离为1,即⊙M的半径为1,
,1),∴M到x轴的距离为1,即⊙M的半径为1, ,(4分)
,(4分)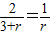 得r=3,
得r=3, ,则⊙N的方程为
,则⊙N的方程为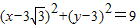 ;(8分)
;(8分)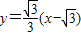 ,即:x-
,即:x- -
- =0,
=0, ,则弦长=2
,则弦长=2 .
.

科目:高中数学 来源: 题型:
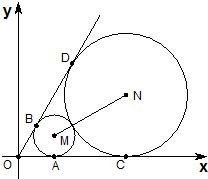 如图,已知圆心坐标为M(
如图,已知圆心坐标为M(| 3 |
| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
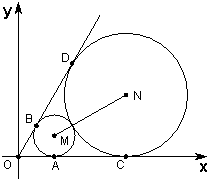 如图,已知圆心坐标为(
如图,已知圆心坐标为(| 3 |
| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:黑龙江省牡丹江一中10-11学年高一下学期期末考试数学(理) 题型:解答题
(本小题满分12分)如图,已知圆心坐标为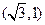 的圆
的圆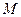 与
与 轴及直线
轴及直线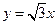 分别相切于
分别相切于 两点,另一圆
两点,另一圆 与圆
与圆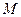 外切,且与
外切,且与 轴及直线
轴及直线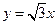 分别相切于
分别相切于 两点.
两点.
(1)求圆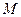 和圆
和圆 的方程;(2)过点
的方程;(2)过点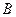 作直线
作直线 的平行线
的平行线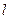 ,求直线
,求直线 被圆
被圆 截得的弦的长度.
截得的弦的长度.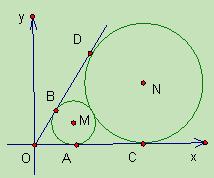
查看答案和解析>>
科目:高中数学 来源:2015届江西南昌八一、中学、麻丘中学高二10月联考数学卷(解析版) 题型:解答题
如图,已知圆心坐标为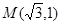 的圆
的圆 与
与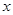 轴及直线
轴及直线 均相切,切点分别为
均相切,切点分别为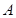 、
、 ,另一圆
,另一圆 与圆
与圆 、
、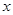 轴及直线
轴及直线 均相切,切点分别为
均相切,切点分别为 、
、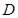 .
.

(1)求圆 和圆
和圆 的方程;
的方程;
(2)过 点作
点作 的平行线
的平行线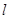 ,求直线
,求直线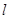 被圆
被圆 截得的弦的长度;
截得的弦的长度;
查看答案和解析>>
科目:高中数学 来源:黑龙江省10-11学年高一下学期期末考试数学(理) 题型:解答题
(本小题满分12分)如图,已知圆心坐标为 的圆
的圆 与
与 轴及直线
轴及直线 分别相切于
分别相切于 两点,另一圆
两点,另一圆 与圆
与圆 外切,且与
外切,且与 轴及直线
轴及直线 分别相切于
分别相切于 两点.
两点.
(1)求圆 和圆
和圆 的方程;(2)过点
的方程;(2)过点 作直线
作直线 的平行线
的平行线 ,求直线
,求直线 被圆
被圆 截得的弦的长度.
截得的弦的长度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com