【题目】下列函数中，既是偶函数，又在区间
上单调递减的是
A．
B．
C．
D．
【答案】C
【解析】主要考查函数的单调性和奇偶性．
对于A，函数
是偶函数，但在区间
上单调递增，故不满足题意；
对于B，函数
是奇函数，在R上单调递增，故不满足题意；
对于C，函数
是偶函数，在区间上单调递减，故满足题意；
对于D，函数
是偶函数，但在区间上有增有减，故不满足题意．故选C．
【规律总结】判断函数的奇偶性，首先求函数的定义域，若定义域不关于原点对称，则函数不具有奇偶性，此时不必求f(－x)．当定义域关于原点对称时，若证明函数具有奇偶性，应运用定义，将f(－x)与f(x)进行比较，有时不易变形时，可直接计算f(－x)±f(x)，判断其是否为零；若证明函数不具有奇偶性，只需找到一组相反量的函数值，不满足f(－a)＝f(a)和f(－a)＝－f(a)即可．
应用题天天练四川大学出版社系列答案科目：高中数学 来源： 题型：
【题目】已知椭圆 
和点P（4，2），直线l经过点P且与椭圆交于A，B两点．
（1）当直线l的斜率为 
时，求线段AB的长度；
（2）当P点恰好为线段AB的中点时，求l的方程．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某校高一（1）班全体男生的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏，但可见部分如图甲所示，据此解答如下问题：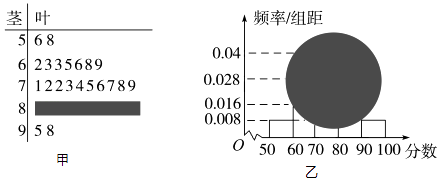 
（1）求该班全体男生的人数；
（2）求分数在[80，90）之间的男生人数，并计算频率公布直方图如图乙中[80，90）之间的矩形的高．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某中学组织了一次高二文科学生数学学业水平模拟测试，学校从测试合格的男、女生中各随机抽取100人的成绩进行统计分析，分别制成了如图所示的男生和女生数学成绩的频率分布直方图．
（Ⅰ）若所得分数大于等于80分认定为优秀，求男、女生优秀人数各有多少人？
（Ⅱ）在（Ⅰ）中的优秀学生中用分层抽样的方法抽取5人，从这5人中任意任取2人，求至少有一名男生的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知平面α及直线a，b，则下列说法正确的是（ ）
A.若直线a，b与平面α所成角都是30°，则这两条直线平行
B.若直线a，b与平面α所成角都是30°，则这两条直线不可能垂直
C.若直线a，b平行，则这两条直线中至少有一条与平面α平行
D.若直线a，b垂直，则这两条直线与平面α不可能都垂直
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数f（x）= 
﹣ax，e为自然对数的底数 （Ⅰ）若函数f（x）的图象在点（e2 ， f（e2））处的切线方程为 3x+4y﹣e2=0，求实数a，b的值；
（Ⅱ）当b=1时，若存在 x1 ， x2∈[e，e2]，使 f（x1）≤f′（x2）+a成立，求实数a的最小值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
