
分析 对x讨论,当x≤1时,运用指数函数的单调性可得;当x>1时,运用对数函数的单调性,即可得到所求解集.
解答 解:由函数f(x)=$\left\{{\begin{array}{l}{{2^{1-x}},\;x≤1}\\{1+{{log}_2}x,\;x>1}\end{array}}$,
可得当x≤1时,f(x)≤3,即为21-x≤3,解得1-x≤log23,
即x≥1-log23,故1-log23≤x≤1;
当x>1时,1+log2x≤3,即log2x≤2,即x≤4,故1<x≤4.
综上可得,x∈[1-log23,4].
故答案为:[1-log23,4].
点评 本题考查分段函数的应用:解不等式,注意运用分类讨论的思想方法,考查指数函数和对数函数的单调性,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (¬p)∨q | B. | p∧q | C. | p∨q | D. | p∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
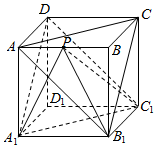
| A. | 平面ACB1∥平面A1C1D,且两平面的距离为$\frac{{\sqrt{3}}}{3}$ | |
| B. | 点P在线段AB上运动,则四面体PA1B1C1的体积不变 | |
| C. | 与所有12条棱都相切的球的体积为$\frac{{\sqrt{2}}}{3}$π | |
| D. | M是正方体的内切球的球面上任意一点,N是△AB1C外接圆的圆周上任意一点,则|MN|的最小值是$\frac{{\sqrt{3}-\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,对大于等于2的自然数m的n次幂进行如图方式的“分裂”,如23的“分裂”中最大的数是5,34的“分裂”中最大的数是29,那么20163的“分裂”中最大的数是20162+2015.(写出算式即可)
如图,对大于等于2的自然数m的n次幂进行如图方式的“分裂”,如23的“分裂”中最大的数是5,34的“分裂”中最大的数是29,那么20163的“分裂”中最大的数是20162+2015.(写出算式即可)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | {-1,1} | C. | {-1} | D. | {0} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com