
【题目】为庆祝党的98岁生日,某高校组织了“歌颂祖国,紧跟党走”为主题的党史知识竞赛。从参加竞赛的学生中,随机抽取40名学生,将其成绩分为六段![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,到如图所示的频率分布直方图.
,到如图所示的频率分布直方图.

(1)求图中![]() 的值及样本的中位数与众数;
的值及样本的中位数与众数;
(2)若从竞赛成绩在![]() 与
与![]() 两个分数段的学生中随机选取两名学生,设这两名学生的竞赛成绩之差的绝对值不大于
两个分数段的学生中随机选取两名学生,设这两名学生的竞赛成绩之差的绝对值不大于![]() 分为事件
分为事件![]() ,求事件
,求事件![]() 发生的概率.
发生的概率.
(3)为了激励同学们的学习热情,现评出一二三等奖,得分在![]() 内的为一等奖,得分在
内的为一等奖,得分在![]() 内的为二等奖, 得分在
内的为二等奖, 得分在![]() 内的为三等奖.若将频率视为概率,现从考生中随机抽取三名,设
内的为三等奖.若将频率视为概率,现从考生中随机抽取三名,设![]() 为获得三等奖的人数,求
为获得三等奖的人数,求![]() 的分布列与数学期望.
的分布列与数学期望.
【答案】(1)0.06;87.5;87.5;(2)![]() ;(3)详见解析
;(3)详见解析
【解析】
(1)根据小矩形的面积之和等于1,列出方程,求得![]() 的值,根据中位数定义估计中位数的范围,在列出方程求解中位数,再根据众数的定义,即可求解.
的值,根据中位数定义估计中位数的范围,在列出方程求解中位数,再根据众数的定义,即可求解.
(2)计算两组的人数,再计算抽取的两人在同一组的概率,即可求解;
(3)根据题意,得到随机变量服从二项分布,再利用二项分布的期望公式,即可求解.
(1)由频率分布直方图可知![]() ,解得
,解得![]() ,
,
可知样本的中位数在第4组中,不妨设为![]() ,
,
则![]() ,解得
,解得![]() ,
,
即样本的中位数为![]() ,
,
由频率分布直方图可知,样本的众数为![]() .
.
(2)由频率分布直方图可知,在![]() 与
与![]() 两个分数段的学生人数分别为
两个分数段的学生人数分别为![]() 和
和![]() ,设中两名学生的竞赛成绩之差的绝对值不大于5分为事件M,
,设中两名学生的竞赛成绩之差的绝对值不大于5分为事件M,
则事件M发生的概率为![]() ,即事件M发生的概率为
,即事件M发生的概率为![]() .
.
(3)从考生中随机抽取三名,则随机变量![]() 为获得三等奖的人数,则
为获得三等奖的人数,则![]() ,
,
由频率分布直方图知,从考升中任抽取1人,此生获得三等奖的概率为![]() ,
,
所以随机变量服从二项分布![]() ,
,
则![]() ,
,
![]() ,
,
所以随机变量的分布列为
| 0 | 1 | 2 | 3 |
| 0.343 | 0.441 | 0.189 | 0.027 |
所以![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某家庭记录了未使用节水龙头50天的日用水量数据(单位:m3)和使用了节水龙头50天的日用水量数据,得到频数分布表如下:
未使用节水龙头50天的日用水量频数分布表
日用 水量 |
|
|
|
|
|
|
|
频数 | 1 | 3 | 2 | 4 | 9 | 26 | 5 |
使用了节水龙头50天的日用水量频数分布表
日用 水量 |
|
|
|
|
|
|
频数 | 1 | 5 | 13 | 10 | 16 | 5 |
(1)在答题卡上作出使用了节水龙头50天的日用水量数据的频率分布直方图:

(2)估计该家庭使用节水龙头后,日用水量小于0.35 m3的概率;
(3)估计该家庭使用节水龙头后,一年能节省多少水?(一年按365天计算,同一组中的数据以这组数据所在区间中点的值作代表.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快递公司收取快递费用的标准是:重量不超过![]() 的包裹收费10元;重量超过
的包裹收费10元;重量超过![]() 的包裹,除收费10元之外,超过
的包裹,除收费10元之外,超过![]() 的部分,每超出
的部分,每超出![]() (不足
(不足![]() ,按
,按![]() 计算)需要再收费5元.该公司近60天每天揽件数量的频率分布直方图如下图所示(同一组数据用该区间的中点值作代表).
计算)需要再收费5元.该公司近60天每天揽件数量的频率分布直方图如下图所示(同一组数据用该区间的中点值作代表).
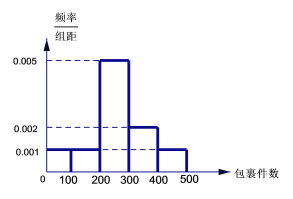
(1)求这60天每天包裹数量的平均值和中位数;
(2)该公司从收取的每件快递的费用中抽取5元作为前台工作人员的工资和公司利润,剩余的作为其他费用.已知公司前台有工作人员3人,每人每天工资100元,以样本估计总体,试估计该公司每天的利润有多少元?
(3)小明打算将![]() 四件礼物随机分成两个包裹寄出,且每个包裹重量都不超过
四件礼物随机分成两个包裹寄出,且每个包裹重量都不超过![]() ,求他支付的快递费为45元的概率.
,求他支付的快递费为45元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点F(1,0),定直线![]() ,动点M到点F的距离与到直线l的距离相等.
,动点M到点F的距离与到直线l的距离相等.
(1)求动点M的轨迹方程;
(2)设点![]() ,过点F作一条斜率大于0的直线交轨迹M于A,B两点,分别连接PA,PB,若直线PA与直线PB不关于x轴对称,求实数t的取值范围.
,过点F作一条斜率大于0的直线交轨迹M于A,B两点,分别连接PA,PB,若直线PA与直线PB不关于x轴对称,求实数t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com