Question

【题目】如图，在四棱锥中，底面为正方形，且,其中，，分别是，，的中点，动点在线段上运动时，下列四个结论：①；②；③面；④面，

其中恒成立的为（ ）

A. ①③ B. ③④ C. ①④ D. ②③

Answer 1

【答案】A

【解析】分析：如图所示，连接AC、BD相交于点O，连接EM，EN．

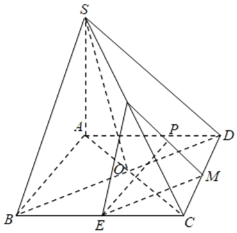
（1）由正四棱锥S﹣ABCD，可得SO⊥底面ABCD，AC⊥BD，进而得到SO⊥AC．可得AC⊥平面SBD．由已知E，M，N分别是BC，CD，SC的中点，利用三角形的中位线可得EM∥BD，MN∥SD，于是平面EMN∥平面SBD，进而得到AC⊥平面EMN，AC⊥EP;（2）由异面直线的定义可知：EP与BD是异面直线，因此不可能EP∥BD；（3）由（1）可知：平面EMN∥平面SBD，可得EP∥平面SBD；（4）由（1）同理可得：EM⊥平面SAC，可用反证法证明：当P与M不重合时，EP与平面SAC不垂直．

详解：

如图所示，连接AC、BD相交于点O，连接EM，EN．

对于（1），由正四棱锥S﹣ABCD，可得SO⊥底面ABCD，AC⊥BD，∴SO⊥AC．

∵SO∩BD=O，∴AC⊥平面SBD，∵E，M，N分别是BC，CD，SC的中点，∴EM∥BD，MN∥SD，而EM∩MN=N，

∴平面EMN∥平面SBD，∴AC⊥平面EMN，∴AC⊥EP．故正确．

对于（2），由异面直线的定义可知：EP与BD是异面直线，不可能EP∥BD，因此不正确；

对于（3），由（1）可知：平面EMN∥平面SBD，∴EP∥平面SBD，因此正确．

对于（4），由（1）同理可得：EM⊥平面SAC，若EP⊥平面SAC，则EP∥EM，与EP∩EM=E相矛盾，因此当P与M不重合时，EP与平面SAC不垂直．即不正确．

故选：A．