
(5分)(2011•陕西)观察下列等式
1=1
2+3+4=9
3+4+5+6+7=25
4+5+6+7+8+9+10=49
照此规律,第五个等式应为 .
5+6+7+8+9+10+11+12+13=81
解析试题分析:根据题意,观察等式的左边,分析可得规律:第n个等式的左边是从n开始的(2n﹣1)个数的和,进而可得答案.
解:根据题意,观察可得,
第一个等式的左边、右边都是1,
第二个等式的左边是从2开始的3个数的和,
第三个等式的左边是从3开始的5个数的和,
…
其规律为:第n个等式的左边是从n开始的(2n﹣1)个数的和,
第五个等式的左边应该是从5开始的9个数的和,即5+6+7+8+9+10+11+12+13,计算可得,其结果为81;
故答案为:5+6+7+8+9+10+11+12+13=81.
点评:本题考查归纳推理,解题时要认真分析题意中的等式,发现其变化的规律,注意验证即可.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
甲、乙、丙三位同学被问到是否去过 、
、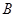 、
、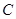 三个城市时,
三个城市时,
甲说:我去过的城市比乙多,但没去过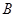 城市;
城市;
乙说:我没去过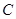 城市;
城市;
丙说:我们三人去过同一城市;
由此可判断乙去过的城市为________.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
观察分析下表中的数据:
| 多面体 | 面数( ) ) | 顶点数( ) ) | 棱数( ) ) |
| 三棱锥 | 5 | 6 | 9 |
| 五棱锥 | 6 | 6 | 10 |
| 立方体 | 6 | 8 | 12 |
 所满足的等式是_________.
所满足的等式是_________.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
1955年,印度数学家卡普耶卡(D.R.Kaprekar)研究了对四位自然数的一种交换:任给出四位数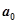 ,用
,用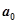 的四个数字由大到小重新排列成一个四位数m,再减去它的反序数n(即将
的四个数字由大到小重新排列成一个四位数m,再减去它的反序数n(即将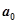 的四个数字由小到大排列,规定反序后若左边数字有0,则将0去掉运算,比如0001,计算时按1计算),得出数
的四个数字由小到大排列,规定反序后若左边数字有0,则将0去掉运算,比如0001,计算时按1计算),得出数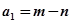 ,然后继续对
,然后继续对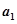 重复上述变换,得数
重复上述变换,得数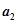 ,…,如此进行下去,卡普耶卡发现,无论
,…,如此进行下去,卡普耶卡发现,无论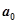 是多大的四位数,只要四个数字不全相同,最多进行k次上述变换,就会出现变换前后相同的四位数t(这个数称为Kaprekar变换的核).通过研究10进制四位数2014可得Kaprekar变换的核为 .
是多大的四位数,只要四个数字不全相同,最多进行k次上述变换,就会出现变换前后相同的四位数t(这个数称为Kaprekar变换的核).通过研究10进制四位数2014可得Kaprekar变换的核为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com