在xOy平面上有一系列的点P
1(x
1,y
1),P
2(x
2,y
2),…,P
n(x
n,y
n),…,对于所有正整数n,点P
n位于函数y=x
2(x≥0)的图象上,以点P
n为圆心的⊙P
n与x轴相切,且⊙P
n与⊙P
n+1又彼此外切,若x
1=1,且x
n+1<x
n.则
nxn=( )
∵圆Pn与P(n+1)相切,且P(n+1)与x轴相切,
所以,R
n=y
n,R
(n+1)=y
(n+1),且两圆心间的距离就等于两半径之和,
即
=y
n+y
n+1整理可得,
-=2
∴
=1+2(n-1)=2n-1
∴
nxn=nxn==
故选C
练习册系列答案
相关习题
科目:高中数学
来源:
题型:
在xOy平面上有一系列的点P
1(x
1,y
1),P
2(x
2,y
2),…,P
n(x
n,y
n)…对于正整数n,点P
n位于函数y=x
2(x≥0)的图象上,以点P
n为圆心的⊙P
n与x轴相切,且⊙P
n与⊙P
n+1又彼此外切,若x
1=1,且x
n+1<x
n.
(1)求证:数列
{}是等差数列;
(2)设⊙P
n的面积为S
n,
Tn=+++…+,求证:
Tn<.
查看答案和解析>>
科目:高中数学
来源:
题型:
(2013•闸北区二模)在xOy平面上有一系列的点P
1(x
1,y
1),P
2(x
2,y
2),…,P
n(x
n,y
n),…,对于所有正整数n,点P
n位于函数y=x
2(x≥0)的图象上,以点P
n为圆心的⊙P
n与x轴相切,且⊙P
n与⊙P
n+1又彼此外切,若x
1=1,且x
n+1<x
n.则
nxn=( )
查看答案和解析>>
科目:高中数学
来源:2011年安徽师大附中高考数学一模试卷(理科)(解析版)
题型:解答题
在xOy平面上有一系列的点P
1(x
1,y
1),P
2(x
2,y
2),…,P
n(x
n,y
n)…对于正整数n,点P
n位于函数y=x
2(x≥0)的图象上,以点P
n为圆心的⊙P
n与x轴相切,且⊙P
n与⊙P
n+1又彼此外切,若x
1=1,且x
n+1<x
n.
(1)求证:数列

是等差数列;
(2)设⊙P
n的面积为S
n,
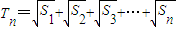
,求证:

.
查看答案和解析>>
科目:高中数学
来源:2013年上海市闸北区高考数学二模试卷(理科)(解析版)
题型:选择题
在xOy平面上有一系列的点P
1(x
1,y
1),P
2(x
2,y
2),…,P
n(x
n,y
n),…,对于所有正整数n,点P
n位于函数y=x
2(x≥0)的图象上,以点P
n为圆心的⊙P
n与x轴相切,且⊙P
n与⊙P
n+1又彼此外切,若x
1=1,且x
n+1<x
n.则

=( )
A.0
B.0.2
C.0.5
D.1
查看答案和解析>>
科目:高中数学
来源:2008年湖北省武汉市华中师大一附中高三五月调考数学试卷(文理合卷)(解析版)
题型:解答题
在xOy平面上有一系列的点P
1(x
1,y
1),P
2(x
2,y
2),…,P
n(x
n,y
n)…对于正整数n,点P
n位于函数y=x
2(x≥0)的图象上,以点P
n为圆心的⊙P
n与x轴相切,且⊙P
n与⊙P
n+1又彼此外切,若x
1=1,且x
n+1<x
n.
(1)求证:数列
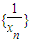
是等差数列;
(2)设⊙P
n的面积为S
n,

,求证:

.
查看答案和解析>>

 是等差数列;
是等差数列;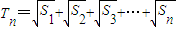 ,求证:
,求证: .
. =( )
=( )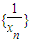 是等差数列;
是等差数列; ,求证:
,求证: .
.